
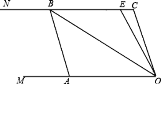
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A,B分别在射线OM,CN上,且∠C=∠OAB=108°,点E在线段CB上,OB平分∠AOE.
(1)图中有哪些与∠AOC相等的角?并说明理由;
(2)若平移AB,那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是cm(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】M 城气象中心测得台风中心在 M 城正北方向 240km 的 P 处,以每小时 45km 的速度向南偏东 30°的 PB 方向移动,距台风中心 150km 的范围内是受台风影响的区域,则 M 城 受台风影响的时间为( )小时.
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出销售单价提高 ![]() 元与总的销售利润y元之间的函数关系式;
元与总的销售利润y元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的两点A、B所表示的数分别是a和b,O为数轴上的原点,如果有理数a,b满足![]()
(1)求a和b的值;
(2)若点P是一个动点,以每秒5个单位长度的速度从点A出发,沿数轴向右运动,请问经过多长时间,点P恰巧到达线段AB的三等分点?
(3)若点C是线段AB的中点,点M以每秒3个单位长度的速度从点C开始向右运动,同时点P以每秒5个单位长度的速度从点A出发向右运动,点N以每秒4个单位长度的速度从点B开始向左运动,点P与点M之间的距离表示为PM,点P与点N之间的距离表示为PN,是否存在某一时刻使得PM+PN=12?若存在,请求出此时点P表示的数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AC、BD交于点O,点P、E分别是直线BD、BC上的动点,且PE=PC,过点E作EF∥AC交直线BD于点F.


(1)如图1,当∠COD=90°时,判断△BEF的形状,并说明理由;
(2)如图2,当点P在线段BO上时,求证:OP=BF;
(3)当∠COD=60°,CD=3时,请直接写出当△PEF成为直角三角形时的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com