
【题目】商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出销售单价提高 ![]() 元与总的销售利润y元之间的函数关系式;
元与总的销售利润y元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
【答案】
(1)解:当销售单价提高x元时,销售量减少了 ![]() 个,
个,
此时单价为(50+x)元,销售量为(30- ![]() )个
)个
则x与y的函数关系式为:y=(50+x-40)(30- ![]() )(0≤ x ≤150)
)(0≤ x ≤150)
答:x与y的函数关系式为:y=(50+x-40)(30- ![]() )(0≤ x ≤150);
)(0≤ x ≤150);
(2)解:将(1)中函数整理后,得:
y=- ![]() +28 x+300=-
+28 x+300=- ![]()
∵- ![]() <0
<0
∴二次函数y=- ![]() +28 x+300有最大值
+28 x+300有最大值
当x=70时,y有最大值,
此时y=1280,
这种书包的单价为:50+70=120
答:当这种书包的单价为120元时,每月的销售利润最大为1280元。
【解析】(1)当销售单价提高x元时,销售量减少了 ![]() 个,此时单价为(50+x)元,销售量为(30-
个,此时单价为(50+x)元,销售量为(30- ![]() )个 ,根据总利润=单个利润×销售数量得出,y与x之间的函数关系式;
)个 ,根据总利润=单个利润×销售数量得出,y与x之间的函数关系式;
(2)为使每月的销售利润最大,求解求函数的最大值问题,把y与x的函数关系式整理成一般形式,然后配成顶点式,根据顶点式从而得出 ,当x=70时,y有最大值,此时y=1280,这种书包的单价为:50+70=120 。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
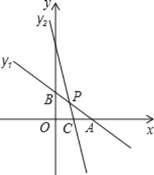
【题目】如图,在平面直角坐标系xOy中,一次函数y1=![]() x+2与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
x+2与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求A、B的坐标;
(2)求△ABO的面积;
(3)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
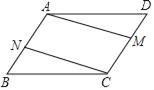
【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM.
(1)求证:BN=DM;
(2)若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
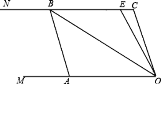
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A,B分别在射线OM,CN上,且∠C=∠OAB=108°,点E在线段CB上,OB平分∠AOE.
(1)图中有哪些与∠AOC相等的角?并说明理由;
(2)若平移AB,那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.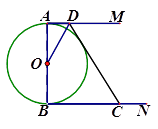
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是线段AB上一点,AC和DG相交于点E.
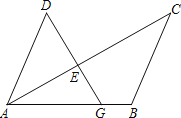
(1)请先作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
(2)然后证明当:AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试说明CD⊥AB.

解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义).
∴DG∥AC(__________________).
∴∠2=∠________(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠________(等量代换).
∴EF∥CD(__________________).
∴∠AEF=∠________ (__________________).
∵EF⊥AB(已知).
∴∠AEF=90°(__________________).
∴∠ADC=90°(__________________).
∴CD⊥AB(__________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2 , 如此继续下去,则正六边形A4B4C4D4E4F4的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com