
【题目】(9分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试说明CD⊥AB.

解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义).
∴DG∥AC(__________________).
∴∠2=∠________(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠________(等量代换).
∴EF∥CD(__________________).
∴∠AEF=∠________ (__________________).
∵EF⊥AB(已知).
∴∠AEF=90°(__________________).
∴∠ADC=90°(__________________).
∴CD⊥AB(__________________).
【答案】解:同位角相等,两直线平行;ACD;ACD;同位角相等,两直线平行;ADC,两直线平行,同位角相等;垂直定义;等量代换;垂直定义.
【解析】试题分析:由DG⊥BC,AC⊥BC,则可得∠DGB=∠ACB=90°,根据平行线的判定定理可得DG∥AC;接下来根据平行线的性质可得:∠2=∠DCA,结合∠1=∠2可得到:∠1=∠DCA,继而推出CD∥EF;接下来根据EF⊥AB,CD∥EF,可得到CD与AB的位置关系.
解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义).
∴DG∥AC(同位角相等,两直线平行).
∴∠2=∠ACD (两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠ACD (等量代换).
∴EF∥CD(同位角相等,两直线平行).
∴∠AEF=∠ADC, (两直线平行,同位角相等).
∵EF⊥AB(已知).
∴∠AEF=90°(垂直定义).
∴∠ADC=90°(等量代换).
∴CD⊥AB(垂直定义).


科目:初中数学 来源: 题型:
【题目】下列调查中,采用的调查方式不适宜的是( )
A. 了解我市中学生的节水意识采取抽样调查的方式
B. 为了调查一个省的环境污染情况,调查该省的省会城市
C. 了解观众对一部电影的评价情况,调查座号为奇数号的现众
D. 了解飞行员视力的达标率采取普查方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于 ![]() AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( ) 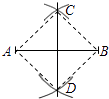
A.矩形
B.菱形
C.正方形
D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国固有领土,位于我国东海,总面积约6340000平方米,数据6340000用科学记数法表示为( )
A.634×104
B.63.4×105
C.6.34×106
D.6.34×107
查看答案和解析>>
科目:初中数学 来源: 题型:
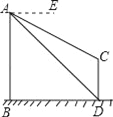
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x (元) | 15 | 20 | 25 | … |
y (件) | 25 | 20 | 15 | … |
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr,本题中π的取值为3.14)

(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,则点A表示的数是 。
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动的情况记录如下:+2,-1,-5,+4,+3,-2.
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动后,Q点运动的路程共有多少?此时点Q所表示的数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com