【题目】如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 
AB的长为半径画弧，两弧相交于C，D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（ ） 
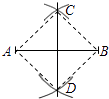
A.矩形
B.菱形
C.正方形
D.等腰梯形
科目：初中数学 来源： 题型：
【题目】下列选项中属于必然事件的是（ ）
A.从只装有黑球的袋子摸出一个白球
B.不在同一直线上的三个点确定一个圆
C.抛掷一枚硬币，第一次正面朝上，第二次反面朝上
D.每年10月1日是星期五
查看答案和解析>>
科目：初中数学 来源： 题型：
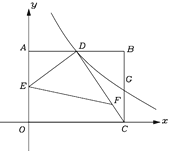
【题目】如图，平面直角坐标系中，矩形OABC的顶点B在第一象限，点C在x轴上，点A在y轴上，D、E分别是AB，OA中点．过点D的双曲线
与BC交于点G．连接DC，F在DC上，且DF：FC=3:1,连接DE，EF．若△DEF的面积为6，则k的值为（ ）．
A. 
B. 
C. 6 D. 10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在□ABCD中，连接对角线
， 
平分线
交
于点
， 
平分线
交
于点
， 
、
交于点
，点
为
上一点，且
。
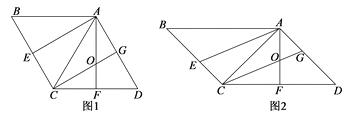
（1）如图1，若
是等边三角形， 
，求□ABCD的面积；
（2）如图2，若
是等腰直角三角形， 
，求证： 
。
查看答案和解析>>
科目：初中数学 来源： 题型：
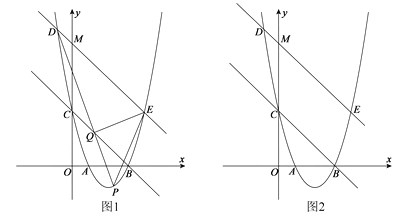
【题目】如图1，在平面直角坐标系
中，抛物线
与
轴交于
两点（点
在点
的左侧），与
轴交于点
，点
的坐标为
，将直线
沿
轴向上平移4个单位长度后恰好经过
两点。
（1）求直线
及抛物线的解析式；
（2）将直线
沿
轴向上平移5个单位长度后与抛物线交于
两点，若点
是抛物线位于直线
下方的一个动点，连接
，交直线
于点
，连接
和
。设
的面积为
，当S取得最大值时，求出此时点
的坐标及
的最大值；
（3）如图2，记（2）问中直线
与
轴交于
点，现有一点
从
点出发，先沿
轴到达
点，再沿
到达
点，已知
点在
轴上运动的速度是每秒2个单位长度，它在直线
上运动速度是1个单位长度。现要使
点按照上述要求到达
点所用的时间最短，请简述确定
点位置的过程，求出点
的坐标，不要求证明。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)填空：
(a－b)(a＋b)＝________；
(a－b)(a2＋ab＋b2)＝________；
(a－b)(a3＋a2b＋ab2＋b3)＝________；
(2)猜想：
(a－b)(an－1＋an－2b＋an－3b2＋…＋abn－2＋bn－1)＝________(其中n为正整数，且n≥2)；
(3)利用(2)猜想的结论计算：
①29＋28＋27＋…＋22＋2＋1；
②210－29＋28－…－23＋22－2.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(9分)如图，已知DG⊥BC，AC⊥BC，EF⊥AB，∠1＝∠2.试说明CD⊥AB.
解：∵DG⊥BC，AC⊥BC(已知)，
∴∠DGB＝∠ACB＝90°(垂直定义).
∴DG∥AC(__________________).
∴∠2＝∠________(两直线平行，内错角相等).
∵∠1＝∠2(已知)，
∴∠1＝∠________(等量代换).
∴EF∥CD(__________________).
∴∠AEF＝∠________ (__________________).
∵EF⊥AB(已知)．
∴∠AEF＝90°(__________________).
∴∠ADC＝90°(__________________)．
∴CD⊥AB(__________________)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2017年元旦期间，某商场打出促销广告，如表所示．
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元，但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠，超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元．
（1）小欣妈妈这两次购物时，所购物品的原价分别为多少？
（2）若小欣妈妈将两次购买的物品一次全部买清，则她是更节省还是更浪费？说说你的理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
