
【题目】顺次连接矩形四边中点所得的四边形一定是( )
A.正方形
B.矩形
C.菱形
D.等腰梯形
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
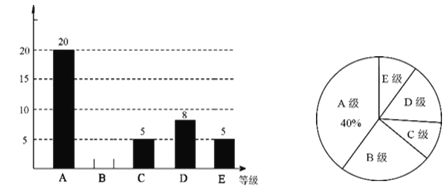
【题目】为了强化同学们的校园安全意识,某学校组织全校3000名同学参加校园安全知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分同学的成绩(等级),统计整理并制作了如下的统计图:
(1)求这次抽样调查的样本容量是 ;
(2)请补全条形统计图;
(3)如果测试成绩(等级)为A,B,C级的定为优秀,请估计该学校参加本次校园安全知识测试成绩(等级)达到优秀的同学的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,采用的调查方式不适宜的是( )
A. 了解我市中学生的节水意识采取抽样调查的方式
B. 为了调查一个省的环境污染情况,调查该省的省会城市
C. 了解观众对一部电影的评价情况,调查座号为奇数号的现众
D. 了解飞行员视力的达标率采取普查方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 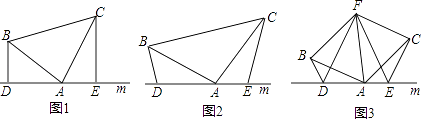
(1)如图(1)已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线 m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=120°.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试证明FD=FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E. 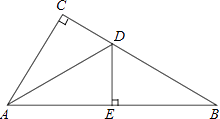
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于 ![]() AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( ) 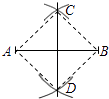
A.矩形
B.菱形
C.正方形
D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
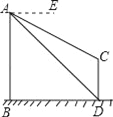
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com