
【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H, 连接OH,求证:∠DHO=∠DCO.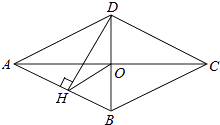
【答案】证明:∵四边形ABCD是菱形, ∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH= ![]() BD=OB,
BD=OB,
∴∠OHB=∠OBH,
又∵AB∥CD,
∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO.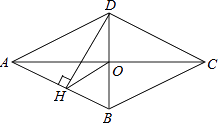
【解析】根据菱形的对角线互相平分可得OD=OB,再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB,然后根据等边对等角求出∠OHB=∠OBH,根据两直线平行,内错角相等求出∠OBH=∠ODC,然后根据等角的余角相等证明即可.
【考点精析】根据题目的已知条件,利用菱形的性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=2,则△A5B5A6的边长为( ) 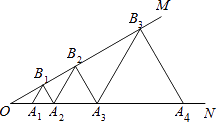
A.8
B.16
C.24
D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一公路上依次有A、B、C城市,A、B城市之间的距离为10千米,B、C城市之间的距离为140千米,一辆快车和一辆慢车分别从A、B两城同时出发驶向C城,快车每小时行驶80千米,慢车每小时行驶60千米.
(1)出发后经过多长时间快车追上慢车?
(2)出发后经过多长时间两车相距5千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的顶点B在第一象限,点C在x轴上,点A在y轴上,D、E分别是AB,OA中点.过点D的双曲线![]() 与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ).
与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ).
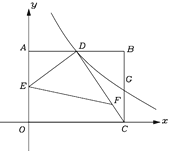
A. ![]() B.
B. ![]() C. 6 D. 10
C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在□ABCD中,连接对角线![]() ,
, ![]() 平分线
平分线![]() 交
交![]() 于点
于点![]() ,
, ![]() 平分线
平分线![]() 交
交![]() 于点
于点![]() ,
, ![]() 、
、![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 上一点,且
上一点,且![]() 。
。
(1)如图1,若![]() 是等边三角形,
是等边三角形, ![]() ,求□ABCD的面积;
,求□ABCD的面积;
(2)如图2,若![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,求证:
,求证: ![]() 。
。
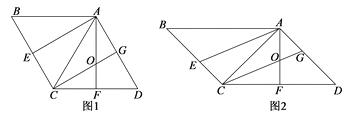
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空:
(a-b)(a+b)=________;
(a-b)(a2+ab+b2)=________;
(a-b)(a3+a2b+ab2+b3)=________;
(2)猜想:
(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)=________(其中n为正整数,且n≥2);
(3)利用(2)猜想的结论计算:
①29+28+27+…+22+2+1;
②210-29+28-…-23+22-2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com