
【题目】如图,已知∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=2,则△A5B5A6的边长为( ) 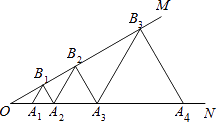
A.8
B.16
C.24
D.32
【答案】D
【解析】解:如图所示:∵△A1B1A2是等边三角形, ∴A1B1=A2B1 , ∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=2,
∴A2B1=2,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3 , B1A2∥B2A3 ,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2 , B3A3=2B2A3 ,
∴A3B3=4B1A2=8,
A4B4=8B1A2=16,
A5B5=16B1A2=32;
故选:D.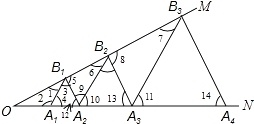
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3 , 以及A2B2=2B1A2 , 得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2得出答案.


科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
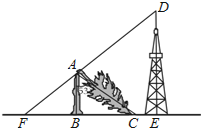
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,采用的调查方式不适宜的是( )
A. 了解我市中学生的节水意识采取抽样调查的方式
B. 为了调查一个省的环境污染情况,调查该省的省会城市
C. 了解观众对一部电影的评价情况,调查座号为奇数号的现众
D. 了解飞行员视力的达标率采取普查方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 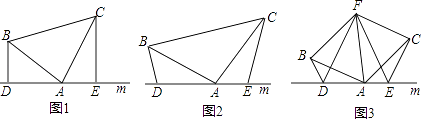
(1)如图(1)已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线 m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=120°.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试证明FD=FE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com