
【题目】已知数轴上的两点A、B所表示的数分别是a和b,O为数轴上的原点,如果有理数a,b满足![]()
(1)求a和b的值;
(2)若点P是一个动点,以每秒5个单位长度的速度从点A出发,沿数轴向右运动,请问经过多长时间,点P恰巧到达线段AB的三等分点?
(3)若点C是线段AB的中点,点M以每秒3个单位长度的速度从点C开始向右运动,同时点P以每秒5个单位长度的速度从点A出发向右运动,点N以每秒4个单位长度的速度从点B开始向左运动,点P与点M之间的距离表示为PM,点P与点N之间的距离表示为PN,是否存在某一时刻使得PM+PN=12?若存在,请求出此时点P表示的数;若不存在,请说明理由.
![]()
【答案】(1)a=-8,b=22;(2)t=2或t=4;(3) 7或![]() .
.
【解析】
(1)根据绝对值以及偶次方的非负性得出a,b的值;
(2)根据点P运动的速度、结合AP:BP=1:2或AP:BP=2:1找出点P的运动时间,设点Q的运动速度为x单位长度/秒,根据路程=速度×时间,即可得出关于x的一元一次方程,解之即可得出结论;
(3)分三种情况:①0<x≤![]() ;②
;②![]() <x≤
<x≤![]() ;③
;③![]() <x时. 结合两点间的距离公式列出相应的方程进行解答即可.
<x时. 结合两点间的距离公式列出相应的方程进行解答即可.
解:(1)a=-8,b=22;
(2)5t=10时,t=2;5t=20时,t=4;
(3) 存在
理由:设运动的时间为x秒,
点C对应的数为7,
点P对应的数为8+5x,
点M对应的数为 7+3x,
点N对应的数为 224x,
则PM=|(8+5x)(7+3x)|=|15+2x|,PN=|(8+5x)(224x)|=|30+9x|.
由PM+PN=12得|15+2x|+|30+9x|=12.
①当0<x≤![]() 时,152x+309x=12,解得:x=3
时,152x+309x=12,解得:x=3![]() ,
,
此时P对应的数为-8+5x=7;
②当![]() <x≤
<x≤![]() 时,152x-30+9x=12,解得:x=
时,152x-30+9x=12,解得:x=![]() 且
且![]() <
<![]() ≤
≤![]() ,
,
此时P对应的数为-8+5x=![]() ;
;
③当![]() <x时,-15+2x-30+9x=12,解得:x=
<x时,-15+2x-30+9x=12,解得:x=![]() 且
且![]() <
<![]() ,舍去;
,舍去;
综上可知,当运动的时间为3秒或![]() 秒时,会使得PM+PN=12,
秒时,会使得PM+PN=12,
此时点P对应的数为 7或![]() .
.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】已知直线y= -![]() +1与x轴、y轴分别交于点A、点B(O为坐标原点),将△ABO绕着点B逆时针旋转60°后,点A恰好落在点C处,那么点C的坐标为___________
+1与x轴、y轴分别交于点A、点B(O为坐标原点),将△ABO绕着点B逆时针旋转60°后,点A恰好落在点C处,那么点C的坐标为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为.
查看答案和解析>>
科目:初中数学 来源: 题型:
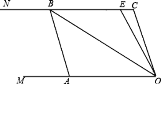
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A,B分别在射线OM,CN上,且∠C=∠OAB=108°,点E在线段CB上,OB平分∠AOE.
(1)图中有哪些与∠AOC相等的角?并说明理由;
(2)若平移AB,那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
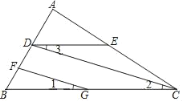
【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是线段AB上一点,AC和DG相交于点E.
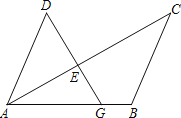
(1)请先作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
(2)然后证明当:AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
(1)如图,FG∥CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG∥CD(已知)
∴∠2=
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC∥
∴∠B+ =180°
又∵∠B=50°
∴∠BDE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com