
【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

【答案】(1)DA∥C E,理由见解析;(2)55°.
【解析】
(1)根据平行线的性质推出AB∥CD,推出∠2=∠ADC,求出∠ADC+∠3=180°,根据平行线的判定推出即可;
(2)求出∠ADC度数,求出∠2=∠ADC=35°,∠FAD=∠AEC=90°,代入∠FAB=∠FAD∠2求出即可.
(1)解:DA∥C E.
理由如下:∵∠1=∠BDC,∴AB∥CD. ∴∠2=∠ADC.
又∵∠2+∠3=180°,∴∠ADC+∠3=180°. ∴DA∥CE.
(2)解:∵DA平分∠BDC,∴∠ADC =![]() ∠BDC =
∠BDC =![]() ∠1 =
∠1 =![]() ×70°=35°.
×70°=35°.
∴∠2=∠ADC=35°.
∵CE⊥AE,AD∥EC, ∴∠FAD=∠AEC=90°.
∴∠FAB=∠FAD-∠2 = 90°-35°= 55°.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】开展“创卫”活动,某校倡议学生利用双休日在“人民公园”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
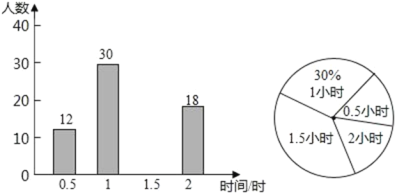
(1)将条形统计图补充完整;
(2)求抽查的学生劳动时间的众数、中位数;
(3)电视台要从参加义务劳动的学生中随机抽取1名同学采访,抽到时参加义务劳动的时间为2小时的同学概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(有阴影部分)面积之和为S2 , 则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
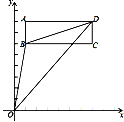
【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的两点A、B所表示的数分别是a和b,O为数轴上的原点,如果有理数a,b满足![]()
(1)求a和b的值;
(2)若点P是一个动点,以每秒5个单位长度的速度从点A出发,沿数轴向右运动,请问经过多长时间,点P恰巧到达线段AB的三等分点?
(3)若点C是线段AB的中点,点M以每秒3个单位长度的速度从点C开始向右运动,同时点P以每秒5个单位长度的速度从点A出发向右运动,点N以每秒4个单位长度的速度从点B开始向左运动,点P与点M之间的距离表示为PM,点P与点N之间的距离表示为PN,是否存在某一时刻使得PM+PN=12?若存在,请求出此时点P表示的数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一根长![]() 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.

(1)求OB的长;
(2)当AA′=1米时,求BB′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com