
【题目】如图,已知∠B=∠C.若AD∥BC,则AD平分∠EAC吗?请说明理由. 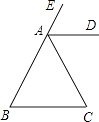
科目:初中数学 来源: 题型:
【题目】某校师生到离校 ![]() 千米远的实习基地培训,甲组师生骑自行车,乙组师生步行,已知骑自行车的速度是步行速度的
千米远的实习基地培训,甲组师生骑自行车,乙组师生步行,已知骑自行车的速度是步行速度的 ![]() 倍. 若甲,乙两组同时出发,结果乙组师生比甲组迟
倍. 若甲,乙两组同时出发,结果乙组师生比甲组迟 ![]() 小时到达目的地,那么乙组师生每小时步行多少千米?
小时到达目的地,那么乙组师生每小时步行多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司要生产若干件新产品,需要精加工后,才能投放市场,现有红星和巨星两个加工厂都想加工这批产品,已知红星厂单独加工比巨星厂单独加工这批产品多用![]() 天,红星厂每天可加工
天,红星厂每天可加工![]() 件产品,巨星厂每天可加工
件产品,巨星厂每天可加工![]() 件产品,公司需付红星厂每天加工费
件产品,公司需付红星厂每天加工费![]() 元,巨星厂每天加工费
元,巨星厂每天加工费![]() 元.
元.
(![]() )这个公司要加工多少件新产品?
)这个公司要加工多少件新产品?
(![]() )在加工过程中,公司需令派一名工程师每天到厂家进行指导,并负担每天
)在加工过程中,公司需令派一名工程师每天到厂家进行指导,并负担每天![]() 元的午餐补助费,公司制定的方案中,选择一种既省钱又省时的加工方案.
元的午餐补助费,公司制定的方案中,选择一种既省钱又省时的加工方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
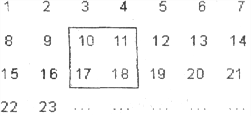
【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去) .
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
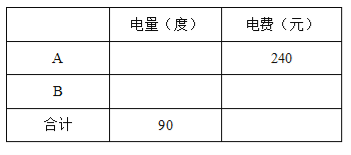
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
猜想与发现:
(3)根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲜花饼是云南的特色小吃,也是中国四大月饼流派滇式月饼的经典代表之一,深受人们喜爱.现某车间要为鲜花饼制作长方体包装盒,已知一个盒子由一个盒身和两个盒底构成,每一张纸板可以做盒身10个或盒底30个.现有纸板100张,应用多少张制作盒身,多少张制作盒底,才能使盒身和盒底正好配套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com