
”¾ĢāÄæ”æĪŖĮĖ·įø»Ķ¬Ń§ĆĒµÄÖŖŹ¶£¬ĶŲÕ¹ŌĶĮŹÓŅ°£¬Ń§Ļ°Ķ¼Źé¹Ż¹ŗĀņĮĖŅ»Š©æĘ¼¼”¢ĪÄѧ”¢ĄśŹ·µČŹé¼®£¬½ųŠŠ×éŗĻ“īÅä³É![]() ”¢
Ӣ![]() Ӣ
”¢![]() ČżÖÖĢ׊ĶŹé¼®£¬·¢·Åøųø÷°ą¼¶µÄĶ¼Źé½Ē¹©Ķ¬Ń§ĆĒŌĶĮ£¬ŅŃÖŖø÷Ģ׊ĶµÄ¹ęøńÓė¼ŪøńČēĻĀ±ķ£ŗ
ČżÖÖĢ׊ĶŹé¼®£¬·¢·Åøųø÷°ą¼¶µÄĶ¼Źé½Ē¹©Ķ¬Ń§ĆĒŌĶĮ£¬ŅŃÖŖø÷Ģ׊ĶµÄ¹ęøńÓė¼ŪøńČēĻĀ±ķ£ŗ
|
|
| |
¹ęøń£Ø±¾/Ģ×£© | 12 | 9 | 7 |
¼Ūøń£ØŌŖ/Ģ×£© | 200 | 150 | 120 |
£Ø1£©ŅŃÖŖ“īÅä![]() ”¢
”¢![]() Į½ÖÖĢ׊ĶŹé¼®¹²15Ģ×£¬Šč¹ŗĀņŹé¼®µÄ»Ø·ŃŹĒ2120ŌŖ£¬ĪŹ
Į½ÖÖĢ׊ĶŹé¼®¹²15Ģ×£¬Šč¹ŗĀņŹé¼®µÄ»Ø·ŃŹĒ2120ŌŖ£¬ĪŹ![]() ”¢
”¢![]() Į½ÖÖĢ׊Ķø÷¶ąÉŁĢ×£æ
Į½ÖÖĢ׊Ķø÷¶ąÉŁĢ×£æ
£Ø2£©ČōĶ¼Źé¹ŻÓĆĄ““īÅäµÄŹé¼®¹²ÓŠ2100±¾£¬ĻÖ½«Ęä“īÅä³É![]() ”¢
”¢![]() Į½ÖÖĢ׊ĶŹé¼®£¬ÕāĮ½ÖÖĢ׊ĶµÄ×ܼŪĪŖ30750ŌŖ£¬Ēó“īÅäŗóŹ£Óą¶ąÉŁ±¾Źé£æ
Į½ÖÖĢ׊ĶŹé¼®£¬ÕāĮ½ÖÖĢ׊ĶµÄ×ܼŪĪŖ30750ŌŖ£¬Ēó“īÅäŗóŹ£Óą¶ąÉŁ±¾Źé£æ
£Ø3£©ČōĶ¼Źé¹ŻÓĆĄ““īÅäµÄŹé¼®¹²ÓŠ122±¾£¬ĻÖ½«Ęä“īÅä³É![]() ”¢
Ӣ![]() Ӣ
”¢![]() ČżÖÖĢ׊ĶŹé¼®¹²13Ģ×£¬ĒŅƻӊŹ£Óą£¬ĒėĒó³öĖłÓŠ“īÅäµÄ·½°ø£®
ČżÖÖĢ׊ĶŹé¼®¹²13Ģ×£¬ĒŅƻӊŹ£Óą£¬ĒėĒó³öĖłÓŠ“īÅäµÄ·½°ø£®
”¾“š°ø”æ£Ø1£©![]() ÖÖ4Ģ×£¬
ÖÖ4Ģ×£¬![]() ÖÖ11Ģ×£»£Ø2£©Ź£ĻĀµÄŹé¼®ĪŖ255±¾£»£Ø3£©
ÖÖ11Ģ×£»£Ø2£©Ź£ĻĀµÄŹé¼®ĪŖ255±¾£»£Ø3£©![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©ÉčAÖÖĢ׊ĶÓŠ![]() Ģ×£¬CÖÖĢ׊ĶÓŠ
Ģ×£¬CÖÖĢ׊ĶÓŠ![]() Ģ×£¬øł¾ŻĮ½ÖÖŹé¼®¹²15Ģ×¼°¹ŗĀņŹé¼®µÄ»Ø·ŃŹĒ2120ŌŖĮŠ·½³Ģ×éĒó½āæÉµĆ£»
Ģ×£¬øł¾ŻĮ½ÖÖŹé¼®¹²15Ģ×¼°¹ŗĀņŹé¼®µÄ»Ø·ŃŹĒ2120ŌŖĮŠ·½³Ģ×éĒó½āæÉµĆ£»
£Ø2£©ÉčAÖŠŹé¼®mĢ×”¢BÖÖŹé¼®nĢ×£¬ÓÉĮ½ÖÖĢ׊ĶµÄ×ܼŪĪŖ30750ŌŖ£¬µĆ³ö![]() £¬
£¬
øł¾Ż“īÅäA”¢BĮ½ÖÖĢ׊ĶŹé¼®ŠčŅŖŹé¼®![]() Ēó½āæÉµĆ£»
Ēó½āæÉµĆ£»
£Ø3£©ÉčAÖÖŹé¼®![]() Ģ×£¬BÖÖŹé¼®
Ģ×£¬BÖÖŹé¼®![]() Ģ×£¬CÖÖŹé¼®
Ģ×£¬CÖÖŹé¼®![]() Ģ×£¬øł¾ŻÓĆĄ““īÅäµÄŹé¼®¹²ÓŠ122±¾µĆ
Ģ×£¬øł¾ŻÓĆĄ““īÅäµÄŹé¼®¹²ÓŠ122±¾µĆ![]() £¬ÓÖ
£¬ÓÖ![]() £¬ĻūČ„
£¬ĻūČ„![]() £¬ŅĄ¾Ż
£¬ŅĄ¾Ż![]() ¾łĪŖ·ĒøŗÕūŹżĒó½āæÉµĆ£®
¾łĪŖ·ĒøŗÕūŹżĒó½āæÉµĆ£®
£Ø1£©Éč![]() ”¢
”¢![]() Į½ÖÖĢ׊Ķø÷ĪŖ
Į½ÖÖĢ׊Ķø÷ĪŖ![]() £¬
£¬![]() Ģ×
Ģ×
ŌņÓŠ![]() £¬½āµĆ
£¬½āµĆ![]() £¬¼“
£¬¼“![]() ÖÖ4Ģ×£¬
ÖÖ4Ģ×£¬![]() ÖÖ11Ģ×
ÖÖ11Ģ×
£Ø2£©Éč![]() ”¢
”¢![]() Į½ÖÖĢ׊Ķø÷ĪŖ
Į½ÖÖĢ׊Ķø÷ĪŖ![]() ”¢
”¢![]() Ģ×£¬ŌņÓŠ
Ģ×£¬ŌņÓŠ![]() £¬
£¬![]() £¬ĖłŅŌæɵƓīÅäŹéµÄ×ÜĮæ
£¬ĖłŅŌæɵƓīÅäŹéµÄ×ÜĮæ![]() £¬ĖłŅŌŹ£ĻĀµÄŹé¼®ĪŖ255±¾
£¬ĖłŅŌŹ£ĻĀµÄŹé¼®ĪŖ255±¾
£Ø3£©Éč![]() ”¢
Ӣ![]() Ӣ
”¢![]() ČżÖÖĢ׊Ķø÷ĪŖ
ČżÖÖĢ׊Ķø÷ĪŖ![]() ”¢
Ӣ![]() Ӣ
”¢![]() Ģ×£¬
Ģ×£¬
ŌņÓŠ![]() £¬ĻūČ„
£¬ĻūČ„![]() µĆ
µĆ![]() £¬¼“
£¬¼“![]() £®
£®
ÓÖ![]() £¬
£¬![]() ¾łĪŖ·ĒøŗÕūŹż£¬ŌņæɵĆ
¾łĪŖ·ĒøŗÕūŹż£¬ŌņæɵĆ![]() »ņ
»ņ![]()


 דŌŖ·»Č«³ĢĶ»Ęʵ¼Į·²āĻµĮŠ“š°ø
דŌŖ·»Č«³ĢĶ»Ęʵ¼Į·²āĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠµÄµćMŗĶĶ¼ŠĪW1£¬W2øų³öČēĻĀ¶ØŅå£ŗµćPĪŖĶ¼ŠĪW1ÉĻŅ»µć£¬µćQĪŖĶ¼ŠĪW2ÉĻŅ»µć£¬µ±µćMŹĒĻ߶ĪPQµÄÖŠµćŹ±£¬³ĘµćMŹĒĶ¼ŠĪW1£¬W2µÄ”°ÖŠĮ¢µć”±£®Čē¹ūµćP£Øx1£¬y1£©£¬Q£Øx2£¬y2£©£¬ÄĒĆ“”°ÖŠĮ¢µć”±MµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£®
£©£®
ŅŃÖŖ£¬µćA£Ø-3£¬0£©£¬B£Ø0£¬4£©£¬C£Ø4£¬0£©£®
£Ø1£©Į¬½ÓBC£¬ŌŚµćD£Ø![]() £¬0£©£¬E£Ø0£¬1£©£¬F£Ø0£¬
£¬0£©£¬E£Ø0£¬1£©£¬F£Ø0£¬![]() £©ÖŠ£¬æÉŅŌ³ÉĪŖµćAŗĶĻ߶ĪBCµÄ”°ÖŠĮ¢µć”±µÄŹĒ______£»
£©ÖŠ£¬æÉŅŌ³ÉĪŖµćAŗĶĻ߶ĪBCµÄ”°ÖŠĮ¢µć”±µÄŹĒ______£»
£Ø2£©ŅŃÖŖµćG£Ø3£¬0£©£¬”ŃGµÄ°ė¾¶ĪŖ2£¬Čē¹ūÖ±Ļßy=-x+1“ęŌŚµćKæÉŅŌ³ÉĪŖµćAŗĶ”ŃGµÄ”°ÖŠĮ¢µć”±£¬ĒóµćKµÄ×ų±ź£»
£Ø3£©ŅŌµćCĪŖŌ²ŠÄ£¬°ė¾¶ĪŖ2×÷Ō²£¬µćNĪŖÖ±Ļßy=2x+4ÉĻµÄŅ»µć£¬Čē¹ū“ęŌŚµćN£¬Ź¹µĆyÖįÉĻµÄŅ»µćæÉŅŌ³ÉĪŖµćNÓė”ŃCµÄ”°ÖŠĮ¢µć”±£¬Ö±½ÓŠ“³öµćNµÄŗį×ų±źµÄȔֵ·¶Ī§£®
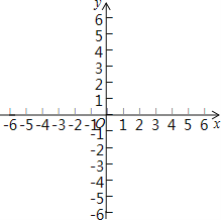
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠĮ½øöŗÆŹż![]() ŗĶ
ŗĶ![]() £¬Čō¶ŌÓŚĆæøöŹ¹ŗÆŹżÓŠŅāŅåµÄŹµŹż
£¬Čō¶ŌÓŚĆæøöŹ¹ŗÆŹżÓŠŅāŅåµÄŹµŹż![]() £¬ŗÆŹż
£¬ŗÆŹż![]() µÄÖµĪŖĮ½øöŗÆŹżÖµÖŠµÄ½ĻŠ”µÄŹż£¬Ōņ³ĘŗÆŹż
µÄÖµĪŖĮ½øöŗÆŹżÖµÖŠµÄ½ĻŠ”µÄŹż£¬Ōņ³ĘŗÆŹż![]() ĪŖÕāĮ½øöŗÆŹż
ĪŖÕāĮ½øöŗÆŹż![]() µÄ½ĻŠ”ÖµŗÆŹż£®ĄżČē£ŗ
µÄ½ĻŠ”ÖµŗÆŹż£®ĄżČē£ŗ![]() £¬Ōņ
£¬Ōņ![]() µÄ½ĻŠ”ÖµŗÆŹżĪŖ
µÄ½ĻŠ”ÖµŗÆŹżĪŖ![]()
£Ø1£©ŗÆŹż![]() ŹĒŗÆŹż
ŹĒŗÆŹż![]() µÄ½ĻŠ”ÖµŗÆŹż£®
µÄ½ĻŠ”ÖµŗÆŹż£®
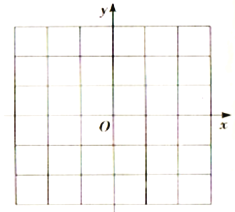
¢ŁŌŚČēĶ¼µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠĮ½³öŗÆŹż![]() µÄĶ¼Ļó£®
µÄĶ¼Ļó£®
¢ŚĒóŗÆŹż![]() µÄĶ¼ĻóÓė
µÄĶ¼ĻóÓė![]() ÖįµÄ½»µć×ų±ź£®
ÖįµÄ½»µć×ų±ź£®
£Ø2£©ŗÆŹż![]() ŹĒŗÆŹż
ŹĒŗÆŹż![]() µÄ½ĻŠ”ÖµŗÆŹż£®
µÄ½ĻŠ”ÖµŗÆŹż£®
¢ŁŠ“³öŗÆŹż![]() µÄĮ½ĢõŠŌÖŹ£®
µÄĮ½ĢõŠŌÖŹ£®
¢Śµ±![]() Ź±£¬ŗÆŹżÖµ
Ź±£¬ŗÆŹżÖµ![]() µÄȔֵ·¶Ī§ĪŖ
µÄȔֵ·¶Ī§ĪŖ![]() £®µ±
£®µ±![]() Č”Ä³øö·¶Ī§ÄŚµÄČĪŅāÖµŹ±£¬
Č”Ä³øö·¶Ī§ÄŚµÄČĪŅāÖµŹ±£¬![]() ĪŖ¶ØÖµ£¬Ö±½ÓŠ“³öĀś×ćĢõ¼žµÄ
ĪŖ¶ØÖµ£¬Ö±½ÓŠ“³öĀś×ćĢõ¼žµÄ![]() µÄȔֵ·¶Ī§¼°Ęä¶ŌÓ¦µÄ
µÄȔֵ·¶Ī§¼°Ęä¶ŌÓ¦µÄ![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×ŪŗĻÓėŹµ¼ł©ĖıߊĪŠż×ŖÖŠµÄŹżŃ§
”°ÖĒ»Ū”±ŹżŃ§Š”×éŌŚæĪĶāŹżŃ§»ī¶ÆÖŠŃŠ¾æĮĖŅ»øöĪŹĢā£¬Ēė°ļĖūĆĒ½ā“š£®
ČĪĪńŅ»£ŗČēĶ¼1£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB=6£¬AD=8£¬E£¬F·Ö±šĪŖAB£¬AD±ßµÄÖŠµć£¬ĖıߊĪAEGFĪŖ¾ŲŠĪ£¬Į¬½ÓCG£®
£Ø1£©ĒėÖ±½ÓŠ“³öCGµÄ³¤ŹĒ______£®
£Ø2£©ČēĶ¼2£¬µ±¾ŲŠĪAEGFČʵćAŠż×Ŗ£Ø±ČČēĖ³Ź±ÕėŠż×Ŗ£©ÖĮµćGĀäŌŚ±ßABÉĻŹ±£¬Ēė¼ĘĖćDFÓėCGµÄ³¤£¬Ķعż¼ĘĖć£¬ŹŌ²ĀĻėDFÓėCGÖ®¼äµÄŹżĮæ¹ŲĻµ£®
£Ø3£©µ±¾ŲŠĪAEGFČʵćAŠż×ŖÖĮČēĶ¼3µÄĪ»ÖĆŹ±£¬£Ø2£©ÖŠDFÓėCGÖ®¼äµÄŹżĮæ¹ŲĻµŹĒ·ń»¹³ÉĮ¢£æĒėĖµĆ÷ĄķÓÉ£®
ČĪĪń¶ž£ŗ”°ÖĒ»Ū”±ŹżŃ§Š”×é¶ŌĶ¼ŠĪµÄŠż×Ŗ½ųŠŠĮĖĶŲÕ¹ŃŠ¾æ£¬ČēĶ¼4£¬ŌŚABCDÖŠ£¬”ĻB=60”ć£¬AB=6£¬AD=8£¬E£¬F·Ö±šĪŖAB£¬AD±ßµÄÖŠµć£¬ĖıߊĪAEGFĪŖĘ½ŠŠĖıߊĪ£¬Į¬½ÓCG£®”°ÖĒ»Ū”±ŹżŃ§Š”×é·¢ĻÖDFÓėCGČŌČ»“ęŌŚ×ÅĢŲ¶ØµÄŹżĮæ¹ŲĻµ£®
£Ø4£©ČēĶ¼5£¬µ±AEGFČʵćAŠż×Ŗ£Ø±ČČēĖ³Ź±ÕėŠż×Ŗ£©£¬ĘäĖūĢõ¼ž²»±äŹ±£¬”°ÖĒ»Ū”±ŹżŃ§Š”×é·¢ĻÖDFÓėCGČŌČ»“ęŌŚ×ÅÕāŅ»ĢŲ¶ØµÄŹżĮæ¹ŲĻµ£®ĒėÄćÖ±½ÓŠ“³öÕāøöĢŲ¶ØµÄŹżĮæ¹ŲĻµ£®





²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÖŠ£¬AC£¬BDŹĒ¶Ō½ĒĻߣ¬”÷ABCŹĒµČ±ßČż½ĒŠĪ£®Ļ߶ĪCDČʵćCĖ³Ź±ÕėŠż×Ŗ60”ćµĆµ½Ļ߶ĪCE£¬Į¬½ÓAE£®
£Ø1£©ĒóÖ¤£ŗAE£½BD£»
£Ø2£©Čō”ĻADC£½30”ć£¬AD£½3£¬BD£½4![]() £®ĒóCDµÄ³¤£®
£®ĒóCDµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
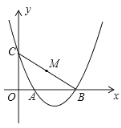
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() ½»xÖįÓŚµćA£¬B£¬½»yÖįÓŚµćC£¬µ±
½»xÖįÓŚµćA£¬B£¬½»yÖįÓŚµćC£¬µ±![]() Ö½Ę¬ÉĻµÄCŃŲ×Å“ĖÅ×ĪļĻßŌĖ¶ÆŹ±£¬Ōņ
Ö½Ę¬ÉĻµÄCŃŲ×Å“ĖÅ×ĪļĻßŌĖ¶ÆŹ±£¬Ōņ![]() Ö½Ę¬ĖęÖ®Ņ²øś×ÅĖ®Ę½ŅĘ¶Æ£¬ÉčÖ½Ę¬ÉĻCBµÄÖŠµćM×ų±źĪŖ
Ö½Ę¬ĖęÖ®Ņ²øś×ÅĖ®Ę½ŅĘ¶Æ£¬ÉčÖ½Ę¬ÉĻCBµÄÖŠµćM×ų±źĪŖ![]() £¬ŌŚ“ĖŌĖ¶Æ¹ż³ĢÖŠ£¬nÓėmµÄ¹ŲĻµŹ½ŹĒ£Ø £©
£¬ŌŚ“ĖŌĖ¶Æ¹ż³ĢÖŠ£¬nÓėmµÄ¹ŲĻµŹ½ŹĒ£Ø £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠĀŠĶøßæĘ¼¼ÉĢĘ·£¬Ć漞µÄŹŪ¼Ū±Č½ų¼Ū¶ą6ŌŖ£¬5¼žµÄ½ų¼ŪĻąµ±ÓŚ4¼žµÄŹŪ¼Ū£¬ĆæĢģæÉŹŪ³ö200¼ž£¬¾ŹŠ³”µ÷²é·¢ĻÖ£¬Čē¹ūĆ漞ÉĢĘ·ÕĒ¼Ū1ŌŖ£¬ĆæĢģ¾Ķ»įÉŁĀō5¼ž£®
£Ø1£©øĆÉĢĘ·µÄŹŪ¼ŪŗĶ½ų¼Ū·Ö±šŹĒ¶ąÉŁŌŖ£æ
£Ø2£©ÉčĆæĢģµÄĻśŹŪĄūČóĪŖwŌŖ£¬Ć漞ÉĢĘ·ÕĒ¼ŪxŌŖ£¬Ōņµ±ŹŪ¼ŪĪŖ¶ąÉŁŌŖŹ±£¬øĆÉĢĘ·ĆæĢģµÄĻśŹŪĄūČó×ī“ó£¬×ī“óĄūČóĪŖ¶ąÉŁŌŖ£æ
£Ø3£©ĪŖŌö¼ÓĻśŹŪĄūČó£¬ÓŖĻś²æĶĘ³öĮĖŅŌĻĀĮ½ÖÖĻśŹŪ·½°ø£ŗ·½°øŅ»£ŗĆ漞ÉĢĘ·ÕĒ¼Ū²»³¬¹ż8ŌŖ£»·½°ø¶ž£ŗĆ漞ÉĢĘ·µÄĄūČóÖĮÉŁĪŖ24ŌŖ£¬Ēė±Č½ĻÄÄÖÖ·½°øµÄĻśŹŪĄūČóøüøߣ¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
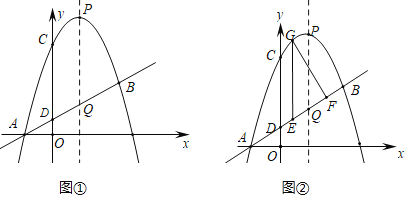
”¾ĢāÄæ”æČēĶ¼¢ŁÅ×ĪļĻßy£½©x2+£Øm©1£©x+mÓėÖ±Ļßy£½kx+k½»ÓŚµćA”¢B£¬ĘäÖŠAµćŌŚxÖįÉĻ£¬ĖüĆĒÓėyÖį½»µć·Ö±šĪŖCŗĶD£¬PĪŖÅ×ĪļĻߵĶ„µć£¬ĒŅµćPׯ×ų±źĪŖ4£¬Å×ĪļĻߵĶŌ³ĘÖį½»Ö±ĻßÓŚµćQ£®
£Ø1£©ŹŌÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾µćQ”¢µćBµÄ×ų±ź£®
£Ø2£©Į¬½ÓPC£¬ČōĖıߊĪCDQPµÄÄŚ²æ£Ø°üĄØ±ß½ēŗĶ¶„µć£©Ö»ÓŠ4øöŗį×ų±ź”¢×Ż×ų±ź¾łĪŖÕūŹżµÄµć£¬ĒókµÄȔֵ·¶Ī§£®
£Ø3£©ČēĶ¼¢Ś£¬ĖıߊĪCDQPĪŖĘ½ŠŠĖıߊĪŹ±£¬
¢ŁĒókµÄÖµ£»
¢ŚE”¢FĪŖĻ߶ĪDBÉĻµÄµć£Øŗ¬¶Ėµć£©£¬ŗį×ų±ź·Ö±šĪŖa£¬a+n£ØnĪŖÕżÕūŹż£©£¬EG”ĪyÖį½»Å×ĪļĻßÓŚµćG£®ĪŹŹĒ·ń“ęŌŚÕżÕūŹżn£¬Ź¹Āś×ćtan”ĻEGF![]() µÄµćEÓŠĮ½øö£æČō“ęŌŚ£¬Ēó³ön£»Čō²»“ęŌŚĖµĆ÷ĄķÓÉ£®
µÄµćEÓŠĮ½øö£æČō“ęŌŚ£¬Ēó³ön£»Čō²»“ęŌŚĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷ŗĶŠ”øÕĶę”°ŹÆĶ·”¢¼ōµ¶”¢²¼”±µÄÓĪĻ·£¬ĆæŅ»¾ÖÓĪĻ·Ė«·½ø÷×ŌĖ껜×ö³ö”°ŹÆĶ·”±”¢”°¼ōµ¶”±”¢”°²¼”±ČżÖ֏֏ʵÄŅ»ÖÖ£¬¹ę¶Ø”°ŹÆĶ·”±Ź¤”°¼ōµ¶”±£¬”°¼ōµ¶”±Ź¤”°²¼”±£¬”°²¼”±Ź¤”°ŹÆĶ·”±£¬ĻąĶ¬µÄŹÖŹĘŹĒŗĶ¾Ö£®
£Ø1£©ÓĆŹ÷ŠĪĶ¼»ņĮŠ±ķ·Ø¼ĘĖćŌŚŅ»¾ÖÓĪĻ·ÖŠĮ½ČĖ»ńŹ¤µÄøÅĀŹø÷ŹĒ¶ąÉŁ£æ
£Ø2£©Čē¹ūĮ½ČĖŌ¼¶Ø£ŗÖ»ŅŖĖĀŹĻČŹ¤Į½¾Ö£¬¾Ķ³ÉĮĖÓĪĻ·µÄÓ®¼Ņ£®ÓĆŹ÷ŠĪĶ¼»ņĮŠ±ķ·ØĒóÖ»½ųŠŠĮ½¾ÖÓĪĻ·±ćÄÜČ·¶ØÓ®¼ŅµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com