
 如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=
如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
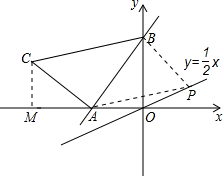 解:(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,
解:(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 4 |
| 5 |
| 2 |


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有10个城市,分别以点A1,A2,…,A10表示,某人从A1出发,按箭头所指示的方向(不准逆向)可以选择任一路线走向其他某个城市.试求:
如图,有10个城市,分别以点A1,A2,…,A10表示,某人从A1出发,按箭头所指示的方向(不准逆向)可以选择任一路线走向其他某个城市.试求:查看答案和解析>>
科目:初中数学 来源: 题型:
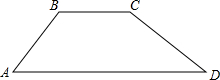 如图,某水库大坝的横截面为梯形ABCD,坝顶宽BC=3米,坝高为2米,背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°.求坝底AD的长度.
如图,某水库大坝的横截面为梯形ABCD,坝顶宽BC=3米,坝高为2米,背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°.求坝底AD的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com