
【题目】如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点. 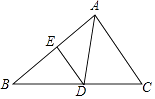
(1)求证:△CAD∽△CBA;
(2)若BD=10,DC=8,求AC的长;
(3)在(2)的条件下,若DE∥AC,AE=4,求BE的长.
【答案】
(1)解:∵在△CAD和△CBA中,
∠DAC=∠B,∠ACD=∠BCA,
∴△CAD∽△CBA
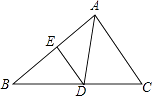
(2)解:∵△CAD∽△CBA,
∴ ![]() =
= ![]() ,即AC2=CD×CB,
,即AC2=CD×CB,
又∵BD=10,DC=8,
∴AC2=8×18=144,
∴AC=±12,
又∵AC>0,
∴AC=12
(3)解:∵DE∥AC,
∴ ![]() =
= ![]() ,
,
又∵BD=10,DC=8,AE=4,
∴ ![]() =
= ![]() ,
,
∴BE=5.
【解析】(1)有两组角对应相等的两个三角形相似,据此判断△CAD∽△CBA即可;(2)根据相似三角形的对应边成比例,得出AC2=CD×CB,再根据BD=10,DC=8,求得AC的长即可;(3)根据平行线分线段成比例定理,由DE∥AC,得出 ![]() =
= ![]() ,再根据BD=10,DC=8,AE=4,求得BE=5即可.
,再根据BD=10,DC=8,AE=4,求得BE=5即可.
【考点精析】关于本题考查的平行线分线段成比例和相似三角形的判定与性质,需要了解三条平行线截两条直线,所得的对应线段成比例;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( ) 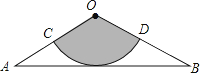
A.10cm
B.15cm
C.10 ![]() cm
cm
D.20 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,则两圆组成的圆环的面积是( ) 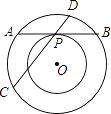
A.16π
B.36π
C.52π
D.81π
查看答案和解析>>
科目:初中数学 来源: 题型:
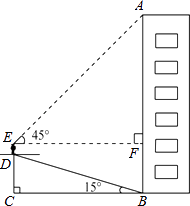
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m) (参考数据:sin15°= ![]() ,cos15°=
,cos15°= ![]() ,tan15°=
,tan15°= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,A,B,C三点的坐标为( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( ) 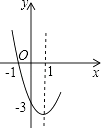
A.﹣1<x<4
B.x<﹣1或x>3
C.x<﹣1或x>4
D.﹣1<x<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 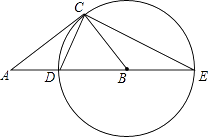
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营一批进价是30元/件的商品,在市场试销中的日销售量y件与销售价x元之间满足一次函数关系.
(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;
x | 35 | 40 | 45 | 50 |
y | 57 | 42 | 27 | 12 |
(2)若日销售利润为P元,根据上述关系写出P关于x的函数关系式,并指出当销售单价x为多少元时,才能获得最大的销售利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x<0)的图象交于A(﹣1,3),B(﹣3,n)两点,直线y=﹣1与y轴交于点C.
(x<0)的图象交于A(﹣1,3),B(﹣3,n)两点,直线y=﹣1与y轴交于点C. 
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com