
【题目】把一个长为![]() 、宽为
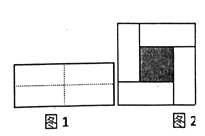
、宽为![]() 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1).
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1).
(1)请用两种不同的方法求图2中阴影部分的面积(直接用含![]() ,
,![]() 的代数式表示)
的代数式表示)
方法1:________,方法2:____;
(2)根据(1)中结论,请你写出下列三个代数式![]() ,
,![]() ,
,![]() 间的等量关系:____;
间的等量关系:____;
(3)根据(2)题中的等量关系,解决如下问题:己知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,请求出
,请求出![]() 的值:
的值:
(4)已知![]() ,请求出
,请求出![]() 的值.
的值.
【答案】(1)(m-n)2;(m+n)2-4mn;(2)(m-n)2=(m+n)2-4mn;(3) 1;(4) ±![]() .
.
【解析】
(1)由题意知,阴影部分为一正方形,其边长正好为m-n.根据正方形的面积公式即可求出图中阴影部分的面积,也可以用大正方形的面积减去四个小长方形的面积由图形可得,大正方形的面积减去四个小长方形的面积正好等于图中阴影部分的面积.
(2)由(1)中的两种方法表示阴影部分的面积故它们相等,从而得到这三个代数式的数量关系;
(3)将两式分别平方后展开,再把两相减即可求出ab的值;
(4)用完全平方公式进行变形即可求出x![]() 的值.
的值.
解:(1)方法1:由题意可得阴影部分为一正方形,其边长正好为m-n,
∴阴影部分的面积(m-n)2,
方法2:图中阴影部分的面积用大正方形的面积减去四个小长方形的面积可得:(m+n)2-4mn,
故答案为:(m-n)2;(m+n)2-4mn;
(2)由图2得:(m+n)2-4mn=(m-n)2;
故答案为:(m-n)2=(m+n)2-4mn.
(3)∵a+b=![]() ,a-b=1,
,a-b=1,
∴(a+b)2=5,(a-b)2=1,
即a2+2ab+b2=5,a2-2ab+b2=1,
两式相减得:4ab=4,
∴ab=1;
(4)∵x+![]() =3,
=3,
∴(x+![]() )2=9,
)2=9,
∴x2+2+![]() =9,
=9,
∴x22+![]() =5,
=5,
∴(x![]() )2=5,
)2=5,
∴x![]() =±
=±![]() .
.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
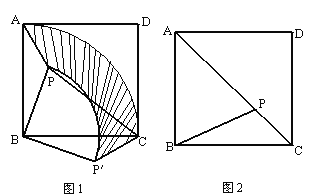
【题目】已知,点P是正方形ABCD内的一点,连PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).
①设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积;
②若PA=2,PB=4,∠APB=135°,求PC的长.
(2)如图2,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)的长方形ABCD中,E点在AD上,且BE=2AE.今分别以BE、CE为折线,将A、D向BC的方向折过去,图(2)为对折后A、B、C、D、E五点均在同一平面上的位置图.若图(2)中,∠AED=15°,则∠BCE的度数为_____.
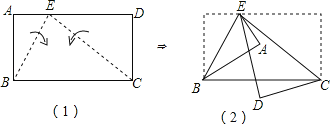
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地,颜色等其他方面完全相同,若背面上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为x,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为y.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出(x,y)所有可能出现的结果.
(2)求取出的两张卡片上的数字之和为偶数的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
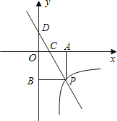
【题目】如图,一次函数![]() 的图象分别交
的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,与反比例函数
,与反比例函数![]() 的图象在第四象限的相交于点
的图象在第四象限的相交于点![]() ,并且
,并且![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,已知
,已知![]() ,且
,且![]()
![]() 求上述一次函数与反比例函数的表达式;
求上述一次函数与反比例函数的表达式;
![]() 求一次函数与反比例函数的另一个交点坐标.
求一次函数与反比例函数的另一个交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某西瓜经营户以![]() 元/千克的价格购进一批小型西瓜,以
元/千克的价格购进一批小型西瓜,以![]() 元/千克的价格出售,每天可售出
元/千克的价格出售,每天可售出![]() 千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价
千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价![]() 元/千克,每天可多售出
元/千克,每天可多售出![]() 千克.另外,每天的房租等固定成本共
千克.另外,每天的房租等固定成本共![]() 元.该经营户要想每天盈利
元.该经营户要想每天盈利![]() 元,应将每千克小型西瓜的售价降低________元.
元,应将每千克小型西瓜的售价降低________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
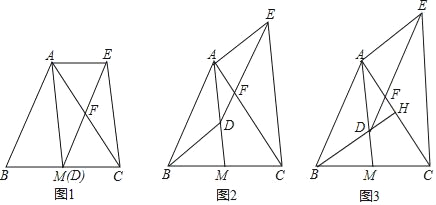
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com