
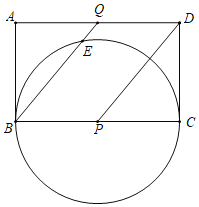
【题目】如图,已知在矩形ABCD中,AB=2,BC=2![]() .点P,Q分别是BC,AD边上的一个动点,连结BQ,以P为圆心,PB长为半径的⊙P交线段BQ于点E,连结PD.
.点P,Q分别是BC,AD边上的一个动点,连结BQ,以P为圆心,PB长为半径的⊙P交线段BQ于点E,连结PD.
(1)若DQ=![]() 且四边形BPDQ是平行四边形时,求出⊙P的弦BE的长;
且四边形BPDQ是平行四边形时,求出⊙P的弦BE的长;
(2)在点P,Q运动的过程中,当四边形BPDQ是菱形时,求出⊙P的弦BE的长,并计算此时菱形与圆重叠部分的面积.
【答案】(1)![]() ;(2)BE=
;(2)BE=![]() ;菱形与圆重叠部分的面积为
;菱形与圆重叠部分的面积为![]() .
.
【解析】
(1)作PT⊥BE于点T,根据垂径定理和勾股定理求BQ的值,再根据相似三角形的判定和性质即可求解;
(2)根据菱形性质和勾股定理求出菱形边长,此时点E和点Q重合,再根据扇形面积公式即可求解.
解:(1)如图:
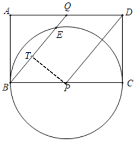
过点P作PT⊥BQ于点T,
∵AB=2,AD=BC=2![]() ,DQ=
,DQ=![]() ,
,
∴AQ=![]() ,
,
在Rt△ABQ中,根据勾股定理可得:BQ=![]() .
.
又∵四边形BPDQ是平行四边形,
∴BP=DQ=![]() ,
,
∵∠AQB=∠TBP,∠A=∠BTP,
∴△AQB∽△TBP,
∴![]()
∴BT=![]() ,
,
∴BE=2BT=![]() .
.
(2)设菱形BPDQ的边长为x,
则AQ=2![]() ﹣x,
﹣x,
在Rt△ABQ中,根据勾股定理,得
AB2+AQ2=BQ2,
即4+(2![]() ﹣x)2=x2,
﹣x)2=x2,
解得x=![]() .
.
∵四边形BPDQ为菱形,∴BP=DP=![]() ,
,
又CP=BC-BP=![]() ,即DP=2CP,
,即DP=2CP,
∴∠DPC=60°,∴∠BPD=120°,
∴连接PQ,易得△BPQ为等边三角形,
∴PQ=BP,
∴点Q也在圆P上,圆P经过点B,D,Q,如图.
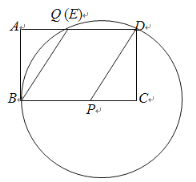
∴点E、Q重合,
∴BE=![]() .
.
∴菱形与圆重叠部分面积即为菱形的面积,
∴S菱形=![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.
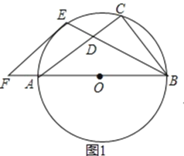
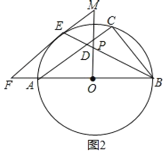

(1)如图1,求证:EF∥AC;
(2)如图2,OP⊥AO交BE于点P,交FE的延长线于点M.求证:△PME是等腰三角形;
(3)如图3,在(2)的条件下:EG⊥AB于H点,交⊙O于G点,交AC于Q点,若sinF=![]() ,EQ=5,求PM的值.
,EQ=5,求PM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与直线y=x+m交于x轴上一点A(﹣1,0),二次函数图象的顶点C(1,﹣4),若二次函数的图象与x轴交于另一点B,与直线y=x+m交于另一点D,求点B与点D之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+3与x轴交于点A(1,0)
(1)求b的值;
(2)若抛物线与x轴的另一个交点为点B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD 中,AB=4,AD=a,点P在AD上,且AP=2,点E是边AB上的动点,以PE为边作直角∠EPF,射线PF交BC于点F,连接EF,给出下列结论:①tan∠PFE=![]() ;②a的最小值为10.则下列说法正确的是( )
;②a的最小值为10.则下列说法正确的是( )
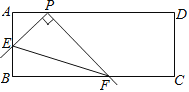
A.①②都对B.①②都错C.①对②错D.①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,等边△ABC中,点D是BC上任一点,以AD为边作∠ADE=∠ADF=60°,分别交AC,AB于点E,F.
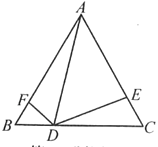
(1)求证:AD2=AEAC.
(2)已知BC=2,设BD的长为x,AF的长为y.
①求y关于x的函数表达式;
②若四边形AFDE外接圆直径为![]() ,求x的值
,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产某品牌的T恤衫成本是每件10元。根据市场调查,以单价13元批发给经销,商销商愿意经销5000件,并且表示每降价0.1元,愿意多经销500件。服装厂决定批发价在不低于11.4元的前提下,将批发价下降0.1x元.
(1)求销售量y与x的关系,并求出x的取值范围;
(2)不考虑其他因素,请问厂家批发单价是多少时所获利润W可以最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com