
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AC��60 cm����A��60�㣬��D�ӵ�C������CA������4 cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2 cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t��(0<t��15)������D��DF��BC�ڵ�F������DE��EF.
(1)��֤��AE��DF��
(2)�ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
(3)��tΪ��ֵʱ����DEFΪֱ�������Σ���ֱ��д�������

���𰸡���1�������������2���ܣ���t��10��ʱ���ı���AEFDΪ���Σ���3����t��![]() ��12��ʱ����DEFΪֱ�������Σ�
��12��ʱ����DEFΪֱ�������Σ�
��������
��1������t��ʾ��CD�Լ�AE�ij���Ȼ����ֱ�ǡ�CDF�У�����ֱ�������ε��������DF�ij�������֤��.
��2����֤�ı���AEFD��ƽ���ı��Σ���AD=AEʱ���ı���AEFD�����Σ��ݴ˼����з������t��ֵ.
��3����DEFΪֱ�������ٵ���DEF��90��ʱ����(2)֪�ı���AEFDΪƽ���ı��Σ�����AD��![]() AE��t����AD��60��4t����60��4t��t�����ɽ�ô�ʱt��12���ڵ���EDF��90��ʱ���ı���EBFDΪ���Σ�����AD��2AE����60��4t��4t����ô�ʱt��
AE��t����AD��60��4t����60��4t��t�����ɽ�ô�ʱt��12���ڵ���EDF��90��ʱ���ı���EBFDΪ���Σ�����AD��2AE����60��4t��4t����ô�ʱt��![]() ��������EFD��90�㣬��E��B�غϣ�D��A�غϣ�������������ڣ�
��������EFD��90�㣬��E��B�غϣ�D��A�غϣ�������������ڣ�
(1)֤�����ڡ�DFC�У���DFC��90�㣬��C��30�㣬DC��4t
��DF��2t
�֡�AE��2t
��AE��DF.
(2)�ܣ��������£�
��AB��BC��DF��BC
��AE��DF
�֡�AE��DF
���ı���AEFDΪƽ���ı��Σ�
���ı���AEFDΪ����ʱ��AE��AD��AC��DC
��60��4t��2t��
���t��10.
�൱t��10��ʱ���ı���AEFDΪ���Σ�
(3)�ٵ���DEF��90��ʱ����(2)֪�ı���AEFDΪƽ���ı��Σ�
��EF��AD
���ADE����DEF��90��
�ߡ�A��60��
���AED��30��
��AD��![]() AE��t.
AE��t.
��AD��60��4t����60��4t��t�����t��12��
�ڵ���EDF��90��ʱ���ı���EBFDΪ���Σ���Rt��AED�У���A��60��
���ADE��30��
��AD��2AE����60��4t��4t�����t��![]() ��
��
������EFD��90�㣬��E��B�غϣ�D��A�غϣ�������������ڣ�
�ʵ�t��![]() ��12��ʱ����DEFΪֱ�������Σ�
��12��ʱ����DEFΪֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���εδ���һ������Լ����ʽ�����������dz��У�С������ڵ�һ������Ӫ��ȫ���ڰ���ij����ϱ�����Ĺ�·�Ͻ��У�������ϼ�����![]() ����������
����������![]() ���������������г�������£�����λ��ǧ�ף�ÿ���г����г˿ͣ�
���������������г�������£�����λ��ǧ�ף�ÿ���г����г˿ͣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ش�
��ش�
��1��С�����һ���˿��͵�Ŀ�ĵ�ʱ��С������������ij����ص�ʲô������������ij����ض�Զ��
��2����С���ij��ÿǧ���ͺ�![]() ����ÿ������
����ÿ������![]() Ԫ����˴γ��������ͷѶ���Ԫ��
Ԫ����˴γ��������ͷѶ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����С����λ����������
����С����λ����������![]() ����
����![]() ����ش����⣺
����ش����⣺
��1����ֱ��д��![]() ��ֵ��
��ֵ��![]() ��
��![]() = ��
= ��
��2����������![]() ����Ӧ�ĵ�ֱ�ΪA��B��C ����PΪ�������ϵĶ��㣬���Ӧ����Ϊ
����Ӧ�ĵ�ֱ�ΪA��B��C ����PΪ�������ϵĶ��㣬���Ӧ����Ϊ![]() ����P�ڵ�A���C֮���˶�ʱ�������˵㣩����AP�� ��PC�� ��
����P�ڵ�A���C֮���˶�ʱ�������˵㣩����AP�� ��PC�� ��
��3���ڣ�1����2���������£�����M��A��������ÿ��1����λ���ȵ��ٶ����յ�C�ƶ�������M�˶���B��ʱ����N��A��������ÿ��3����λ������C���˶���N�㵽��C�����������ͬ�����ٶȷ��ص�A�����M �ƶ�ʱ��Ϊt�룬����N��ʼ�˶������ú�t�Ĵ���ʽ��ʾM��N�����ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����̲Ļعˣ�
���Ͻ̲�������һ�����֣�����ͨ�����ڹ۲췢������糿����������ĸ��ƣ���ô��������꽵�٣��������ˡ����������ƣ���������١����������ѧ��ѧϰ�����У����Ǿ����������ķ���̽�����ɣ�
����ѧ���⣩
�ı�����4�����㣬����������ڲ��ٻ�n���㣬�����⣨n+4������Ϊ���㻭�����Σ���ô�����Լ��ö��ٸ������������Σ�
������̽����
Ϊ�˽��������⣬���ǿ��Դ�n=1��n=2��n=3�Ⱦ���ġ����������֣�̽�������Լ��õ������θ����ı仯���ɣ�
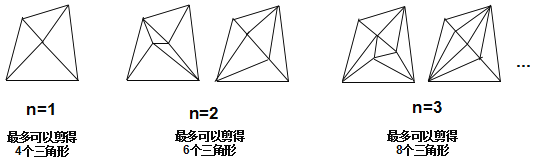
����������
��1�����ı�������4����ʱ�������õ������θ���Ϊ______________��
��2���㷢�ֵı仯�����ǣ��ı����ڵĵ�ÿ����1���������õ�����������______����
��3�����룺���ı����ڵ�ĸ���Ϊnʱ�������Լ���_______________�������Σ�������ͨ���Լ����εĹ۲졢�����������һ���̽����������Ĺ��ɡ���������˼�뷽����Ϊ���ɣ�
��������չ��
���㳢���ù��ɵķ���̽��4+6+8+10+��+2n+��2n+2���ĺ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016��Ȫ���г��������п����������ȡijУ5λͬѧһ���������Ĵ����ֱ�Ϊ��158��160��154��158��170�������������ݵõ��Ľ�������������������
A. ƽ����Ϊ160 B. ��λ��Ϊ158 C. ����Ϊ158 D. ����Ϊ20.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꣬���ŵ�������Ŀ��ٷ�չ�������̰�������ռ����ݼ��������ı�������������������ҵ�Ʊ���ij��վ�õ�����ͳ�Ʊ���
��� | 2014 | 2015 | 2016 | 2017��Ԥ�ƣ� |
��ݼ��������ڼ��� | 140 | 207 | 310 | 450 |
���̰��������ڼ��� | 98 | 153 | 235 | 351 |
��1����ѡ���ʵ���ͳ��ͼ������2014��2017�ꡰ���̰�������ռ���ꡰ��ݼ��������İٷֱȣ���ȷ��1%����
��2����2018�ꡰ��ݼ����������ﵽ675�ڼ�����������С����̰�������ԼΪ�����ڼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���߳�Ϊa�������η����α���Ϊ�߳�Ϊa�����Σ����������ε�һ��Ա�֮��ľ���Ϊh�����ǰ�![]() ��ֵ����������ε����α���������磬���α�����������ͼ2��״�����Խ���BD�ֳ�2���ȱ������Σ�����������ε����α����Ϊ2��
��ֵ����������ε����α���������磬���α�����������ͼ2��״�����Խ���BD�ֳ�2���ȱ������Σ�����������ε����α����Ϊ2��![]() ����ͼ3����������16���߳�Ϊ1��С��������ɣ��α���Ϊ���Σ���AEF��A��E��F�Ǹ�㣩ͬʱ�α�Ϊ��A'E'F'����������ε����α����k=
����ͼ3����������16���߳�Ϊ1��С��������ɣ��α���Ϊ���Σ���AEF��A��E��F�Ǹ�㣩ͬʱ�α�Ϊ��A'E'F'����������ε����α����k=![]() ����
����![]() _______��
_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���A�����ƶ�1����λ�õ�B����B�����ƶ�(n��1)����λ�õ���C����C�����ƶ�(n��2)(nΪ������)����λ�õ���D����A��B��C��D�ֱ��ʾ������a��b��c��d��
(1)��n��1ʱ��B��C����ľ���Ϊ ����λ��C��D����ľ���Ϊ ����λ��
(2)��a����10��n��1ʱ����A��B������2����λ����/����ٶ����������˶���ͬʱC��D������1����λ����/����ٶ����������˶��������˶�ʱ��Ϊt�룬��A��B���㶼�˶���C��D����֮��(����C��D�������غ�)ʱ����t��ȡֵ��Χ��
(3)a��b��c��d�ĸ����Ļ�Ϊ�����������ĸ����ĺ������е��������ĺ���ȣ�aΪ����.��n�ֱ�ȡ1��2��3��4������50ʱ����Ӧ��a��ֵ�ֱ���Ϊa1��a2��a3��������a50����a1��a2��a3��������a50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
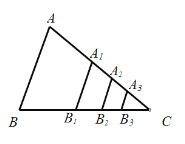
����Ŀ����ͼ����ABC�����Ϊ1���ֱ�ȡAC��BC���ߵ��е�A1��B1�����ı���A1ABB1�����Ϊ![]() ���ٷֱ�ȡA1C��B1C���е�A2��B2��ȡA2C��B2C���е�A3��B3������ȡ��ȥ��������һͼ�Σ���ֱ�۵ؼ����
���ٷֱ�ȡA1C��B1C���е�A2��B2��ȡA2C��B2C���е�A3��B3������ȡ��ȥ��������һͼ�Σ���ֱ�۵ؼ����![]() �� ��
�� ��
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com