
【题目】已知:![]() 是最小的两位正整数,且
是最小的两位正整数,且![]() 满足
满足![]() ,请回答问题:
,请回答问题:
(1)请直接写出![]() 的值:
的值:![]() ,
,![]() = .
= .
(2)在数轴上![]() 所对应的点分别为A、B、C ,点P为该数轴上的动点,其对应的数为
所对应的点分别为A、B、C ,点P为该数轴上的动点,其对应的数为![]() ,点P在点A与点C之间运动时(包含端点),则AP= ,PC= .
,点P在点A与点C之间运动时(包含端点),则AP= ,PC= .
(3)在(1)(2)的条件下,若点M从A出发,以每秒1个单位长度的速度向终点C移动,当点M运动到B点时,点N从A出发,以每秒3个单位长度向C点运动,N点到达C点后,再立即以同样的速度返回点A,设点M 移动时间为t秒,当点N开始运动后,请用含t的代数式表示M、N两点间的距离.
【答案】(1)a=-26,b=-10,c=1;
(2)AP=m+26,PC=10-m;
(3)分五种情况:①当16<t≤24时, MN= -2t+48;②当24<t≤28时, MN=2t-48;③当28<t≤30时, MN=-4t+120;④当30<t≤36时, MN=4t-120;⑤当36<t≤40时, MN=3t-84.
【解析】
(1)根据题意可以求得a、b、c的值,从而可以解答本题;
(2)根据数轴上两点的距离公式:AB=xB-xA,可以表示AP和PC的长;
(3)先计算t的取值,因为点M从A出发,以每秒1个单位长度的速度向终点C移动,且AC=36,所以需要36秒完成,又因为当点M运动到B点时,即16秒后,点N从A出发,以每秒3个单位长度向C点运动,所以点N还需要运动24秒,所以一共需要40秒,再分别计算M、N两次相遇的时间,分五种情况讨论,根据图形结合数轴上两点的距离表示MN的长.
解:(1)∵c是最小的两位正整数,a,b满足(a+26)2+|b+c|=0,
∴c=10,a+26=0,b+c=0,
∴a=-26,b=-10,c=10,
故答案为:-26,-10,10;
(2)∵点P为点A和C之间一点,其对应的数为x(![]() ),
),
∴AP=m+26,PC=10-m;
故答案为:m+26,10-m;
(3)点N运动的总时间为:2(36÷3)=12×2=24,
此时,t=24+16=40,
设t秒时,M、N第一次相遇,
3(t-16)=t,
t=24,
分五种情况:
①当16<t≤24时,如图1,M在N的右侧,此时MN=t-3(t-16)=-2t+48,

②当24<t≤28时,如图2,M在N的左侧,此时MN=3(t-16)-t=2t-48,

③M、N第二次相遇(点N从C点返回时):t+3(t-16)=36×2,
t=30,
当28<t≤30时,如图3,点M在N的左侧,此时MN=36×2-t-3(t-16)=-4t+120,

④当30<t≤36时,如图4,点M在N的右侧,此时MN=3(t-16)-36-(36-t)=4t-120,

⑤当36<t≤40时,如图5,点M在点C处,此时MN=3(t-16)-36=3t-84,



 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
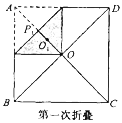
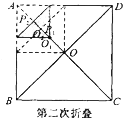
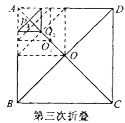
【题目】如图,正方形纸片ABCD的边长为![]() ,对角线相交于点O,第1次将纸片折叠,使点A与点O重合,折痕与AO交于点P1;设P1O的中点为O1,第2次将纸片折叠,使点A与点O1重合,折痕与AO交于点P2;设P2O1的中点为O2,第3次将纸片折叠,使点A与点O2重合,折痕与AO交于点P3;…;设Pn-1On-2的中点为On-1,第n次将纸片折叠,使点A与点On-1重合,折痕与AO交于点Pn(n>2),则APn的长为__________.
,对角线相交于点O,第1次将纸片折叠,使点A与点O重合,折痕与AO交于点P1;设P1O的中点为O1,第2次将纸片折叠,使点A与点O1重合,折痕与AO交于点P2;设P2O1的中点为O2,第3次将纸片折叠,使点A与点O2重合,折痕与AO交于点P3;…;设Pn-1On-2的中点为On-1,第n次将纸片折叠,使点A与点On-1重合,折痕与AO交于点Pn(n>2),则APn的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科学技术的发展,信息化、网络化时代的到来,很多农产品改变了原来的销售模式,实行了网上销售,刚大学毕业的小韦把自己家的红薯产品也放到网上,他原来计划每天卖出150千克,由于各种原因,实际每天的销售量与计划量相比有出入,下表是国庆小长假期间的销售情况(超出部分记为正,不足记为负,单位:千克)
时间 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据上表前四天一共卖出了多少千克?
(2)销售量最多的一天与最少的一天分别是多少千克?
(3)若每千克按2. 6元出售,并需付运费平均每千克0. 3元,则小韦国庆小长假期间一共收入多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界卫生组织预计:到2025年,全世界将会有一半人面临用水危机,为了倡导“节约用水,从我做起”,某县政府决定对县直属机关300户家庭一年的月平均用水量进行调查,调查小组抽查了部分家庭月平均用水量(单位:吨),绘制条形图和扇形图如图所示.
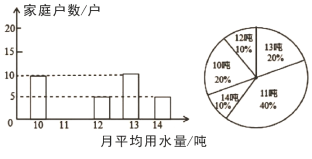
(1)请将条形统计图补充完整;
(2)这些家庭月平均用水量数据的平均数是_______,众数是______,中位数是_______;
(3)根据样本数据,估计该县直属机关300户家庭的月平均用水量不超过12吨的约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节期间某商场对顾客实行优惠,规定如下:若一次购物不超过 300 元(含 300 元),按标价九折优惠,若一次购物超过 300 元,但不超过 800 元(含 800 元),所有商品按标价给予八折优惠,若一次购物超过 800 元,其中 800 元按八折优惠之外,超过 800 元的部分给予六折优惠.
(1)若某人一次购物货款为x元(x>1000),打折后应付多少元?
(2)若某人两次购物分别付款180 元和 1000 元,如果他合起来一次去购买同样的商品,他还可以节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用小立方块搭一个几何体,使它从正面和上面看到的形状如图所示,从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数,请问:
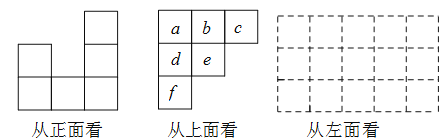
(1)![]() ,
,![]() 各表示几? 答:
各表示几? 答:![]() _____ ,
_____ ,![]() _____;
_____;
(2)这个几何体最少由_____个小立方块搭成,最多由____个小立方块搭成;
(3)能搭出满足条件的几何体共有____种情况,其中从左面看这个几何体的形状图共有____种,请在所给网格图中画出其中的任意一种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请直接写出结果;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com