
【题目】某出租车一天上午从省实验中学门口出发沿着南北向的文化路营运,向北为正,向南为负,行驶里程(单位:![]() )依次顺序记录如下:+18,-5,-2,+3,+10,-9,+12,-3,-7,-15.
)依次顺序记录如下:+18,-5,-2,+3,+10,-9,+12,-3,-7,-15.
(1)将最后一名乘客送到目的地,出租车在出发地什么方向?距离出发地多远?
(2)不超过3千米时,按照步价收费8元,超过3千米的部分,每千米1.5元,司机上午的营业额是多少?
科目:初中数学 来源: 题型:
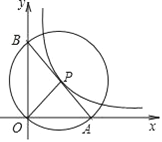
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若代数式(4x2-mx-3y+4)-(8nx2-x+2y-3)的值与字母x的取值无关,求代数式(-m2+2mn-n2)-2(mn-3m2)+3(2n2-mn)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎做一道数学题,“已知两个多项式![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.
(1)小马虎看答案以后知道![]() ,请你替小马虎求出系数“
,请你替小马虎求出系数“![]() ”;
”;
(2)在(1)的基础上,小马虎已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求小马虎求出
,要求小马虎求出![]() 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() .请你替小马虎求出“
.请你替小马虎求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四个结论中正确的是_____(填写序号).
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1;
④如果5是方程M的一个根,那么![]() 是方程N的一个根.
是方程N的一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4,表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
![]()
若数轴上数-3表示的点与数1表示的点重合.(请依据此情境解决下列问题)
①则数轴上数3表示的点与数 表示的点重合.
②若点![]() 到与原点的距离是5个单位长度,并且
到与原点的距离是5个单位长度,并且![]() ,
,![]() 两点经折叠后重合,则点
两点经折叠后重合,则点![]() 点表示的数是 .
点表示的数是 .
③若数轴上![]() ,
,![]() 两点之间的距离为2018,并且
两点之间的距离为2018,并且![]() ,
,![]() 两点经折叠后重合,如果
两点经折叠后重合,如果![]() 点表示的数比
点表示的数比![]() 点表示的数大,则
点表示的数大,则![]() 点表示的数是 ,则
点表示的数是 ,则![]() 点表示的数是 .
点表示的数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
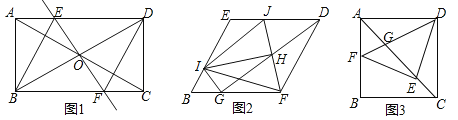
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后
的纪录如下:回答下列问题:

(1)这8筐白菜中最接近标准重量的这筐白菜重 千克;
(2)若这批白菜以2元 ∕ 千克的价格出售,则这批白菜一共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2x+c(a≠0)与x轴、y轴分别交于点A,B,C三点,已知点A(﹣2,0),点C(0,﹣8),点D是抛物线的顶点.
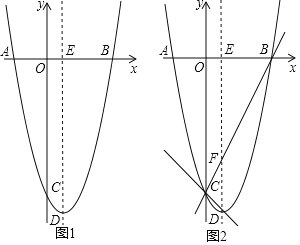
(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
(3)如图2,设BC交抛物线的对称轴于点F,作直线CD,点M是直线CD上的动点,点N是平面内一点,当以点B,F,M,N为顶点的四边形是菱形时,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com