
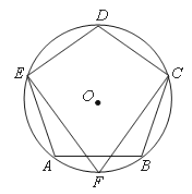
【题目】如图,☉O是正五边形ABCDE的外接圆,F是![]() 的中点,连接CF,EF.
的中点,连接CF,EF.
(1)请直接写出∠CFE= °;
(2)求证:EF=CF;
(3)若☉O的半径为5,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
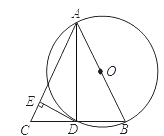
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两只捕捞船同时在上午![]() 从
从![]() 港出海捕鱼.甲船以
港出海捕鱼.甲船以![]() 的速度沿西偏北
的速度沿西偏北![]() 方向前进,乙船以
方向前进,乙船以![]() 的速度沿东北方向前进.甲船在
的速度沿东北方向前进.甲船在![]() 航行到达
航行到达![]() 处,此时甲船发现部分渔具丢在乙船上,于是甲船快速(匀速)沿北偏东
处,此时甲船发现部分渔具丢在乙船上,于是甲船快速(匀速)沿北偏东![]() 的方向追赶,结果两船在
的方向追赶,结果两船在![]() 处相遇.(其他因素不作考虑)
处相遇.(其他因素不作考虑)
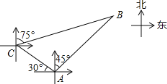
![]() 问乙船在什么时候被甲船追上;
问乙船在什么时候被甲船追上;
![]() 求甲船追赶乙船的速度.
求甲船追赶乙船的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为________;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10=( )

A. 4π B. 3π C. 2π D. π
查看答案和解析>>
科目:初中数学 来源: 题型:
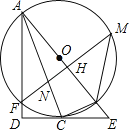
【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=![]() ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块含30°角的三角板的直角顶点放在反比例函数y=﹣![]() (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标坐标为_____.
(x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com