
【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10=( )

A. 4π B. 3π C. 2π D. π
【答案】D
【解析】
图1,作辅助线构建正方形OECF,设圆O的半径为r,根据切线长定理表示出AD和BD的长,利用AD+BD=5列方程求出半径r=![]() (a、b是直角边,c为斜边),运用圆面积公式=πr2求出面积=π;图2,先求斜边上的高CD的长,再由勾股定理求出AD和BD,利用半径r=
(a、b是直角边,c为斜边),运用圆面积公式=πr2求出面积=π;图2,先求斜边上的高CD的长,再由勾股定理求出AD和BD,利用半径r=![]() (a、b是直角边,c为斜边)求两个圆的半径,从而求出两圆的面积和=π;图3,继续求高DM和CM、BM,利用半径r=
(a、b是直角边,c为斜边)求两个圆的半径,从而求出两圆的面积和=π;图3,继续求高DM和CM、BM,利用半径r=![]() (a、b是直角边,c为斜边)求三个圆的半径,从而求出三个圆的面积和.
(a、b是直角边,c为斜边)求三个圆的半径,从而求出三个圆的面积和.
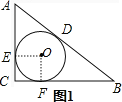
解:(1)图1,过点O做OE⊥AC,OF⊥BC,垂足为E、F,则∠OEC=∠OFC=90°
∵∠C=90°
∴四边形OECF为矩形
∵OE=OF
∴矩形OECF为正方形
设圆O的半径为r,则OE=OF=r,AD=AE=3-r,BD=4-r
∴3-r+4-r=5,r=1
∴S1=π×12=π
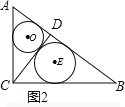
(2)图2,由S△ABC=![]() ×3×4=
×3×4=![]() ×5×CD
×5×CD
∴CD=![]()
由勾股定理得:AD=![]() ,BD=5-
,BD=5-![]() =
=![]()
由(1)得:⊙O的半径=![]() ,⊙E的半径=
,⊙E的半径=![]()
∴S1+S2=π×(![]() )2+π×(
)2+π×(![]() )2=π
)2=π
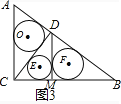
(3)图3,由S△CDB=![]() ×
×![]() ×
×![]() =
=![]() ×4×MD
×4×MD
∴MD=![]()
由勾股定理得:CM=![]() ,MB=4-
,MB=4-![]() =
=![]()
由(1)得:⊙O的半径![]() ,:⊙E的半径=
,:⊙E的半径=![]() :⊙F的半径=
:⊙F的半径=![]()
∴S1+S2+S3=π×(![]() )2+π×(
)2+π×(![]() )2+π×(
)2+π×(![]() )2=π
)2=π
∴图4中的S1+S2+S3+S4=π
则S1+S2+S3+…+S10=π
故选:D.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
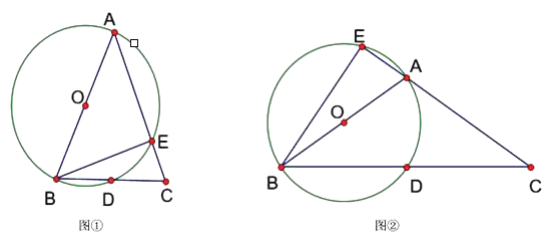
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
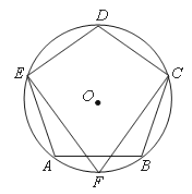
【题目】如图,☉O是正五边形ABCDE的外接圆,F是![]() 的中点,连接CF,EF.
的中点,连接CF,EF.
(1)请直接写出∠CFE= °;
(2)求证:EF=CF;
(3)若☉O的半径为5,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
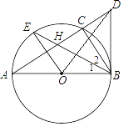
【题目】如图,AB是⊙O的直径,C是⊙O是一点,过点B作⊙O的切线,与AC延长线交于点D,连接BC,OE//BC交⊙O于点E,连接BE交AC于点H。(1)求证:BE平分∠ABC;(2)连接OD,若BH=BD=2,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
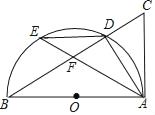
【题目】如图,在Rt△ABC中,∠BAC=90°,以边AB为直径作⊙O,交斜边BC于D,E在弧![]() 上,连接AE、ED、DA,连接AE、ED、DA.
上,连接AE、ED、DA,连接AE、ED、DA.
(1)求证:∠DAC=∠AED;
(2)若点E是![]() 的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com