
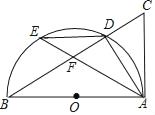
【题目】如图,在Rt△ABC中,∠BAC=90°,以边AB为直径作⊙O,交斜边BC于D,E在弧![]() 上,连接AE、ED、DA,连接AE、ED、DA.
上,连接AE、ED、DA,连接AE、ED、DA.
(1)求证:∠DAC=∠AED;
(2)若点E是![]() 的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
【答案】(1)详见解析;(2)DF=2.
【解析】
(1)根据圆周角定理得到AD⊥BC,根据余角的性质和圆周角定理即可得到结论;
(2)根据等腰三角形的性质得到CA=CF,根据相似三角形的性质即可得到结论.
(1)证明:∵AB是⊙O的直径,
∴AD⊥BC,
∵∠BAC=90°,
∴∠CAD+∠BAD=∠BAD+∠B=90°,
∴∠CAD=∠B,
∵∠E=∠ABD,
∴∠DAC=∠AED;
(2)∵点E是![]() 的中点,
的中点,
∴∠BAE=∠EAD,
∵∠CFA=∠ABC+∠BAE,∠CAE=∠CDA+∠EAD,
∴∠CFA=∠CAE,
∴CA=CF,
∵∠BAC=∠ADB=90°,
∴∠ACD=∠BCA,
∴△ADC∽△BAC,
∴![]() ,
,
即AC2=BC×CD=(5+4)×4=36,
解得AC=6,
∴CA=CF=6,
∴DF=CA﹣CD=2.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
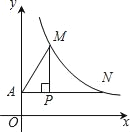
【题目】如图,过点P(2,![]() )作x轴的平行线交y轴于点A,交双曲线
)作x轴的平行线交y轴于点A,交双曲线![]() 于点N,作PM⊥AN交双曲线
于点N,作PM⊥AN交双曲线![]() 于点M,连接AM,若PN=4.
于点M,连接AM,若PN=4.
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10=( )

A. 4π B. 3π C. 2π D. π
查看答案和解析>>
科目:初中数学 来源: 题型:
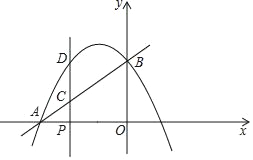
【题目】如图,在直角坐标系中,O是坐标原点,直线AB交x轴于点A(﹣4,0),交y轴于点B,抛物线y=ax2+2ax+3(a≠0)经过A,B两点.P是线段AO上的一动点,过点P作PC⊥x轴交直线AB于点C,交抛物线于点D.
(1)求a及AB的长.
(2)连结PB,若tan∠ABP=![]() ,求点P的坐标.
,求点P的坐标.
(3)连结BD,以BD为边作正方形BDEF,是否存在点P使点E恰好落在抛物线的对称轴上?若存在,请求出点P的坐标;若不存在,请说明理由.
(4)连结OC,若S△BDC:S△OBC=1:2,将线段BD绕点D按顺时针方向旋转,得到DB′.则在旋转的过程中,当点A,B到直线DB′的距离和最大时,请直接写出点B′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块含30°角的三角板的直角顶点放在反比例函数y=﹣![]() (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标坐标为_____.
(x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。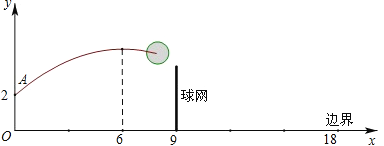
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用48米长的竹篱笆在空地上,围成一个绿化场地,现有两种设计方案,一种是围成正方形的场地;另一种是围成圆形场地.现请你选择,围成________(圆形、正方形两者选一)场在面积较大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 yx2bxc(b,c均为常数),当x1时,函数有最小值.甲乙丙三位同学继续研究,得出以下结论:甲:该函数的最小值为3;乙:1是方程x2bxc0的一个根;丙:当x2时,y4.若这三个结论中只有一个是错误的,那么得出错误结论的同学是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com