
【题目】用48米长的竹篱笆在空地上,围成一个绿化场地,现有两种设计方案,一种是围成正方形的场地;另一种是围成圆形场地.现请你选择,围成________(圆形、正方形两者选一)场在面积较大.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
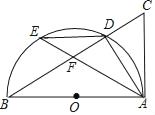
【题目】如图,在Rt△ABC中,∠BAC=90°,以边AB为直径作⊙O,交斜边BC于D,E在弧![]() 上,连接AE、ED、DA,连接AE、ED、DA.
上,连接AE、ED、DA,连接AE、ED、DA.
(1)求证:∠DAC=∠AED;
(2)若点E是![]() 的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知二次函数![]() .
.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
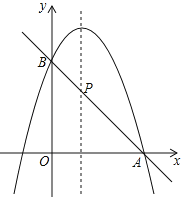
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
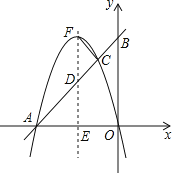
【题目】如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.
(1)求点A的坐标;
(2)设二次函数图象的顶点为F,其对称轴与直线AB及x轴分别交于点D和点E,若△FCD与△AED相似,求此二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有![]() 棵枇杷树.每棵平均产量为
棵枇杷树.每棵平均产量为![]() 千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量
千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量![]() 千克,若设增种
千克,若设增种![]() 棵枇杷树,投产后果园枇杷的总产量为
棵枇杷树,投产后果园枇杷的总产量为![]() 千克,则
千克,则![]() 与
与![]() 之间的函数关系式为________.
之间的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元,经调查发现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下所示:
每个商品的售价x(元) | … | 30 | 40 | 50 | … |
每天的销售量y(个) | 100 | 80 | 60 | … |
(1)求y与x之间的函数表达式;
(2)设商场每天获得的总利润为w(元),求w与x之间的函数表达式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com