
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌжБЯпABНЛxжсгкЕуAЃЈЉ4ЃЌ0ЃЉЃЌНЛyжсгкЕуBЃЌХзЮяЯпy=ax2+2ax+3ЃЈaЁй0ЃЉОЙ§AЃЌBСНЕуЃЎPЪЧЯпЖЮAOЩЯЕФвЛЖЏЕуЃЌЙ§ЕуPзїPCЁЭxжсНЛжБЯпABгкЕуCЃЌНЛХзЮяЯпгкЕуDЃЎ
ЃЈ1ЃЉЧѓaМАABЕФГЄЃЎ
ЃЈ2ЃЉСЌНсPBЃЌШєtanЁЯABP=![]() ЃЌЧѓЕуPЕФзјБъЃЎ
ЃЌЧѓЕуPЕФзјБъЃЎ
ЃЈ3ЃЉСЌНсBDЃЌвдBDЮЊБпзїе§ЗНаЮBDEFЃЌЪЧЗёДцдкЕуPЪЙЕуEЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉСЌНсOCЃЌШєSЁїBDCЃКSЁїOBC=1ЃК2ЃЌНЋЯпЖЮBDШЦЕуDАДЫГЪБеыЗНЯђа§зЊЃЌЕУЕНDBЁфЃЎдђдка§зЊЕФЙ§ГЬжаЃЌЕБЕуAЃЌBЕНжБЯпDBЁфЕФОрРыКЭзюДѓЪБЃЌЧыжБНгаДГіЕуBЁфЕФзјБъЃЎ
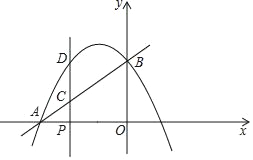
ЁОД№АИЁПЃЈ1ЃЉa=Љ![]() ЃЌABЕФГЄЮЊ5ЃЛЃЈ2ЃЉЕуPЕФзјБъЃЈЃ1.5ЃЌ0ЃЉЃЛЃЈ3ЃЉEЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЧщПіДцдкЃЌЕуPЕФзјБъЮЊЃЈ
ЃЌABЕФГЄЮЊ5ЃЛЃЈ2ЃЉЕуPЕФзјБъЃЈЃ1.5ЃЌ0ЃЉЃЛЃЈ3ЃЉEЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЧщПіДцдкЃЌЕуPЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈЉ4ЃЌ0ЃЉЃЛЃЈ4ЃЉЕБЕуAЃЌBЕНжБЯпDBЁфЕФОрРыКЭзюДѓЪБЕуBЁфЕФзјБъЮЊЃЈЉ
ЃЌ0ЃЉЛђЃЈЉ4ЃЌ0ЃЉЃЛЃЈ4ЃЉЕБЕуAЃЌBЕНжБЯпDBЁфЕФОрРыКЭзюДѓЪБЕуBЁфЕФзјБъЮЊЃЈЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉАбЕуAЃЈЉ4ЃЌ0ЃЉДњШыХзЮяЯпy=ax2+2ax+3ЗНГЬМДПЩЧѓНтЃЛ
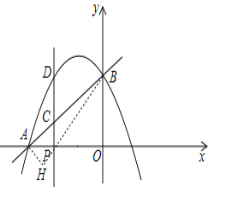
ЃЈ2ЃЉШчЭМЃЌСЌНгBPЃЌзїAHЁЭPBгкHЃЌЩшЕуPЕФзјБъЮЊЃЈxЃЌ0ЃЉЃЎдђOP=ЉxЃЌAP=4+xЃЌBP=![]() ЃЎПЩжЄУїЁїAPHЁзЁїBPOЃЌгЩЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌСаЗНГЬВЂЧѓНтМДПЩЕУЕННсТлЃЛ
ЃЎПЩжЄУїЁїAPHЁзЁїBPOЃЌгЩЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌСаЗНГЬВЂЧѓНтМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉШчЭМЫљЪОЃЌе§ЗНаЮDBFEЕФEЕудкХзЮяЯпЕФЖдГЦжсЩЯЃЌжЄУїRtЁїBHDЁеRtЁїENDЃЈAASЃЉЃЌгУEN=BHМДПЩЧѓНтЃЛ
ЃЈ4ЃЉРћгУЁїBDCКЭЁїOBCЪЧЕШИпВЛЕШЕзЕФСНИіШ§НЧаЮЃЌЧѓГіCD![]() OB
OB![]() ЃЌЧѓГіDЕузјБъЃЈmЃЌ
ЃЌЧѓГіDЕузјБъЃЈmЃЌ![]() ЃЉЃЌАбЕуDЕФзјБъДњШыЖўДЮКЏЪ§ЗНГЬy
ЃЉЃЌАбЕуDЕФзјБъДњШыЖўДЮКЏЪ§ЗНГЬy![]() x2
x2![]() x+3ПЩвдЧѓГіDЕузјБъЮЊЃКDЃЈЉ2ЃЌ3ЃЉЃЌЖјBЃЈ0ЃЌ3ЃЉдђBDЁЮxжсЃЛдкRtЁїB'MDжаЃЌB'D=BD=2ЃЌtanЁЯB'DP
x+3ПЩвдЧѓГіDЕузјБъЮЊЃКDЃЈЉ2ЃЌ3ЃЉЃЌЖјBЃЈ0ЃЌ3ЃЉдђBDЁЮxжсЃЛдкRtЁїB'MDжаЃЌB'D=BD=2ЃЌtanЁЯB'DP![]() ЃЌдђЃКB'M
ЃЌдђЃКB'M![]() ЃЌDM
ЃЌDM![]() ЃЌМДПЩЧѓНтЃЎ
ЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉАбЕуAЃЈЉ4ЃЌ0ЃЉДњШыХзЮяЯпy=ax2+2ax+3ЗНГЬНтЕУЃКa![]() ЃЌЖўДЮКЏЪ§ЕФБэДяЪНЮЊЃКy
ЃЌЖўДЮКЏЪ§ЕФБэДяЪНЮЊЃКy![]() x2
x2![]() x+3ЃЌдђBзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
x+3ЃЌдђBзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
ЁпOA=4ЃЌOB=3ЃЌгЩЙДЙЩЖЈРэЕУЃКAB=5ЃЌдђЖўДЮКЏЪ§БэДяЪНЮЊЃКy![]() x2
x2![]() x+3ЃЌЖдГЦжсЮЊx=Љ1ЃЎ
x+3ЃЌЖдГЦжсЮЊx=Љ1ЃЎ
Д№ЃКa![]() ЃЌABЕФГЄЮЊ5ЃЎ
ЃЌABЕФГЄЮЊ5ЃЎ
ЃЈ2ЃЉШчЭМЃЌСЌНгBPЃЌзїAHЁЭPBгкHЃЎдкRtЁїABHжаЃЌAB=5ЃЌtanЁЯABP![]() ЃЌПЩЕУЃКAH
ЃЌПЩЕУЃКAH![]() ЃЌBH=2
ЃЌBH=2![]() ЃЌЩшЕуPЕФзјБъЮЊЃЈxЃЌ0ЃЉЃЌдђOP=ЉxЃЌAP=4+xЃЌBP=
ЃЌЩшЕуPЕФзјБъЮЊЃЈxЃЌ0ЃЉЃЌдђOP=ЉxЃЌAP=4+xЃЌBP=![]() =
=![]() ЃЎ
ЃЎ
ЁпЁЯAPH=ЁЯBPOЃЌЁЯAHP=ЁЯPOB=90ЁуЃЌЁрЁїAPHЁзЁїBPOЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌећРэЕУЃК4x2+72x+99=0ЃЌЁрЃЈ2x+3ЃЉЃЈ2x+33ЃЉ=0ЃЌНтЕУЃКx=Ѓ1.5ЃЌЛђx=Ѓ16.5ЃЈЩсШЅЃЉЃЌЁрЕуPЕФзјБъЮЊЃЈЃ1.5ЃЌ0ЃЉЃЎ
ЃЌећРэЕУЃК4x2+72x+99=0ЃЌЁрЃЈ2x+3ЃЉЃЈ2x+33ЃЉ=0ЃЌНтЕУЃКx=Ѓ1.5ЃЌЛђx=Ѓ16.5ЃЈЩсШЅЃЉЃЌЁрЕуPЕФзјБъЮЊЃЈЃ1.5ЃЌ0ЃЉЃЎ
ЃЈ3ЃЉШчЭМЫљЪОЃЌе§ЗНаЮDBFEЕФEЕудкХзЮяЯпЕФЖдГЦжсЩЯЃЌДгEЕузїENЁЭPDЃЌзїDHЁЭyжсЃЌдђRtЁїBHDЁеRtЁїENDЃЈAASЃЉЃЌЁрEN=BHЃЌЩшPЕузјБъЮЊЃЈaЃЌ0ЃЉЃЌдђDЁЂEЕуЕФзјБъЗжБ№ЮЊЃЈaЃЌ![]() a2
a2![]() a+3ЃЉЁЂЃЈЉ1ЃЌyЃЉЃЌBH=3ЉЃЈ
a+3ЃЉЁЂЃЈЉ1ЃЌyЃЉЃЌBH=3ЉЃЈ![]() a2
a2![]() a+3ЃЉ=EN=Љ1ЉaЃЌНтЕУЃКx
a+3ЃЉ=EN=Љ1ЉaЃЌНтЕУЃКx![]() ЃЌx=Љ4ЃЎ
ЃЌx=Љ4ЃЎ
Д№ЃКEЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЧщПіДцдкЃЌЕуPЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈЉ4ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЛђЃЈЉ4ЃЌ0ЃЉЃЎ

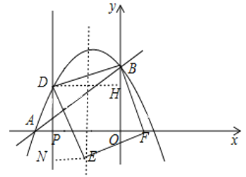
ЃЈ4ЃЉЕБBDа§зЊЕНШчЭМDB'ЕФЮЛжУЪБЃЌЕуAЃЌBЕНжБЯпDB'ЕФОрРыКЭзюДѓЃЌДЫЪБABЁЭB'DЃЌЙ§ЕуB'ЯђPDКЭxжсзїДЙЯпЃЌМДB'MЁЭDPЃЌB'NЁЭxжсЃЌгЩAЁЂBСНЕузјБъПЩЕУABЕФжБЯпЗНГЬЮЊЃКy![]() x+3ЃЌдђtanЁЯBAO
x+3ЃЌдђtanЁЯBAO![]() ЃЌЩшPЕузјБъЮЊЃЈmЃЌ0ЃЉЃЌдђCЃЈmЃЌ
ЃЌЩшPЕузјБъЮЊЃЈmЃЌ0ЃЉЃЌдђCЃЈmЃЌ![]() m+3ЃЉЃЎ
m+3ЃЉЃЎ
ЁпЁїBDCКЭЁїOBCЪЧЕШИпВЛЕШЕзЕФСНИіШ§НЧаЮЃЌЖј1ЃК2ШєSЁїBDCЃКSЁїOBC=1ЃК2ЃЌЁрCD![]() OB
OB![]() ЃЌдђDЕуyзјБъ=CЕуyзјБъ
ЃЌдђDЕуyзјБъ=CЕуyзјБъ![]() ЃЌМДЃКDЃЈmЃЌ
ЃЌМДЃКDЃЈmЃЌ![]() ЃЉЃЌАбЕуDЕФзјБъЃЈmЃЌ
ЃЉЃЌАбЕуDЕФзјБъЃЈmЃЌ![]() ЃЉДњШыЖўДЮКЏЪ§ЗНГЬy
ЃЉДњШыЖўДЮКЏЪ§ЗНГЬy![]() x2
x2![]() x+3ЃЌНтЕУЃКm=Љ2ЃЌАбmжЕДњШыЃЌМДDЕузјБъЮЊЃКDЃЈЉ2ЃЌ3ЃЉЃЌPЃЈЉ2ЃЌ0ЃЉЃЎ
x+3ЃЌНтЕУЃКm=Љ2ЃЌАбmжЕДњШыЃЌМДDЕузјБъЮЊЃКDЃЈЉ2ЃЌ3ЃЉЃЌPЃЈЉ2ЃЌ0ЃЉЃЎ
ЁпBЃЈ0ЃЌ3ЃЉдђBDЁЮxжсЃЌЁрBDЁЭDCЃЎ
ЁпBDЁЭDCЃЌABЁЭB'DЃЌDPЁЭAPЃЌЁрЁЯB'DP=ЁЯBAOЃЌЁрtanЁЯB'DP=tanЁЯBAO![]() ЃЎдкRtЁїB'MDжаЃЌB'D=BD=2ЃЌtanЁЯB'DP
ЃЎдкRtЁїB'MDжаЃЌB'D=BD=2ЃЌtanЁЯB'DP![]() ЃЌдђЃКB'M
ЃЌдђЃКB'M![]() ЃЌDM
ЃЌDM![]() ЃЌдђЃКB'ЕФКсзјБъЮЊ=xPЉB'M=Љ2
ЃЌдђЃКB'ЕФКсзјБъЮЊ=xPЉB'M=Љ2![]() ЃЌB'ЕФзнзјБъЮЊ=yDЉDM=3
ЃЌB'ЕФзнзјБъЮЊ=yDЉDM=3![]() ЃЎ
ЃЎ
Д№ЃКЕБЕуAЃЌBЕНжБЯпDB'ЕФОрРыКЭзюДѓЪБЕуB'ЕФзјБъЮЊЃЈ![]() ЃЉЃЎ
ЃЉЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
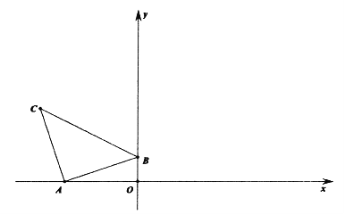
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжагаRtЁїABCЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌA(-3,0)ЃЌB(0,1)ЃЌC(m,n)ЁЃ
(1)ЧыжБНгаДГіCЕузјБъЁЃ
(2)НЋЁїABC биxжсЕФе§ЗНЯђЦНвЦtИіЕЅЮЛЃЌ![]() ЁЂ
ЁЂ![]() СНЕуЕФЖдгІЕуЁЂе§КУТфдкЗДБШР§КЏЪ§
СНЕуЕФЖдгІЕуЁЂе§КУТфдкЗДБШР§КЏЪ§![]() дкЕквЛЯѓЯоФкЭМЯѓЩЯЁЃЧыЧѓГіtЃЌkЕФжЕЁЃ
дкЕквЛЯѓЯоФкЭМЯѓЩЯЁЃЧыЧѓГіtЃЌkЕФжЕЁЃ
(3)дк(2)ЕФЬѕМўЯТЃЌЮЪЪЧЗёДцxжсЩЯЕФЕуMКЭЗДБШР§КЏЪ§![]() ЭМЯѓЩЯЕФЕуNЃЌЪЙЕУвд
ЭМЯѓЩЯЕФЕуNЃЌЪЙЕУвд![]() ЁЂ
ЁЂ![]() ЁЂMЁЂNЮЊЖЅЕуЕФЫФБпаЮЙЙГЩЦНааЫФБпаЮ?ШчЙћДцдкЃЌЧыЧѓГіЫљгаТњзуЬѕМўЕФЕуMКЭЕуNЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ЁЂMЁЂNЮЊЖЅЕуЕФЫФБпаЮЙЙГЩЦНааЫФБпаЮ?ШчЙћДцдкЃЌЧыЧѓГіЫљгаТњзуЬѕМўЕФЕуMКЭЕуNЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCжаЃЌAB=ACЃЌвдABЮЊжБОЖЕФЁбOНЛBCгкЕуDЃЌНЛACгкЕуEЃЎ
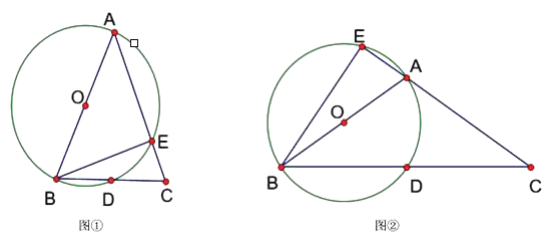
(1)ЕБЁЯBACЮЊШёНЧЪБЃЌШчЭМЂйЃЌЧѓжЄЃКЁЯCBE=![]() ЁЯBACЃЛ
ЁЯBACЃЛ
(2)ЕБЁЯBACЮЊЖлНЧЪБЃЌШчЭМЂкЃЌCAЕФбгГЄЯпгыЁбOЯрНЛгкЕуEЃЌ(1)жаЕФНсТлЪЧЗёШдШЛГЩСЂЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
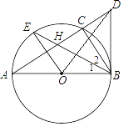
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌCЪЧЁбOЪЧвЛЕуЃЌЙ§ЕуBзїЁбOЕФЧаЯпЃЌгыACбгГЄЯпНЛгкЕуDЃЌСЌНгBCЃЌOE//BCНЛЁбOгкЕуEЃЌСЌНгBEНЛACгкЕуHЁЃЃЈ1ЃЉЧѓжЄЃКBEЦНЗжЁЯABCЃЛЃЈ2ЃЉСЌНгODЃЌШєBH=BD=2ЃЌЧѓODЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌгыxжсЕФвЛИіНЛЕузјБъЮЊ
ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌгыxжсЕФвЛИіНЛЕузјБъЮЊ![]() ЃЌХзЮяЯпЕФЖдГЦжсЪЧ
ЃЌХзЮяЯпЕФЖдГЦжсЪЧ![]() ЯТСаНсТлжаЃК
ЯТСаНсТлжаЃК
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЗНГЬ
ЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ![]() ХзЮяЯпгыxжсЕФСэвЛИіНЛЕузјБъЮЊ
ХзЮяЯпгыxжсЕФСэвЛИіНЛЕузјБъЮЊ![]() ЃЛ
ЃЛ![]() ШєЕу
ШєЕу![]() дкИУХзЮяЯпЩЯЃЌдђ
дкИУХзЮяЯпЩЯЃЌдђ![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФга![]() ЁЁЁЁ
ЁЁЁЁ![]()

A. 5Иі B. 4Иі C. 3Иі D. 2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋвЛеХе§ЗНаЮжНЦЌЕФ4ИіНЧМєШЅ4ИіДѓаЁвЛбљЕФаЁе§ЗНаЮЃЌШЛКѓелЦ№РДОЭПЩвджЦГЩвЛИіЮоИЧЕФГЄЗНЬхжНКаЃЌЩшетИіе§ЗНаЮжНЦЌЕФБпГЄЮЊaЃЌетИіЮоИЧЕФГЄЗНЬхКазгИпЮЊhЃЎ
ЃЈ1ЃЉШєa=18cmЃЌh=4cmЃЌдђетИіЮоИЧГЄЗНЬхКазгЕФЕзУцУцЛ§ЮЊ ЃЛ
ЃЈ2ЃЉгУКЌaКЭhЕФДњЪ§ЪНБэЪОетИіЮоИЧГЄЗНЬхКазгЕФШнЛ§V= ЃЛ
ЃЈ3ЃЉШєa=18cmЃЌЪдЬНОПЃКЕБhдНДѓЃЌЮоИЧГЄЗНЬхКазгЕФШнЛ§VОЭдНДѓТ№ЃПЧыОйР§ЫЕУїЃЛетИіЮоИЧГЄЗНЬхКазгЕФзюДѓШнЛ§ЪЧ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
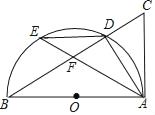
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯBACЃН90ЁуЃЌвдБпABЮЊжБОЖзїЁбOЃЌНЛаББпBCгкDЃЌEдкЛЁ![]() ЩЯЃЌСЌНгAEЁЂEDЁЂDAЃЌСЌНгAEЁЂEDЁЂDAЃЎ
ЩЯЃЌСЌНгAEЁЂEDЁЂDAЃЌСЌНгAEЁЂEDЁЂDAЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯDACЃНЁЯAEDЃЛ
ЃЈ2ЃЉШєЕуEЪЧ![]() ЕФжаЕуЃЌAEгыBCНЛгкЕуFЃЌЕБBDЃН5ЃЌCDЃН4ЪБЃЌЧѓDFЕФГЄЃЎ
ЕФжаЕуЃЌAEгыBCНЛгкЕуFЃЌЕБBDЃН5ЃЌCDЃН4ЪБЃЌЧѓDFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
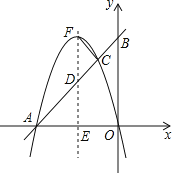
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bxЃЈaЃМ0ЃЉЕФЭМЯѓЙ§зјБъдЕуOЃЌгыxжсЕФИКАыжсНЛгкЕуAЃЌЙ§AЕуЕФжБЯпгыyжсНЛгкBЃЌгыЖўДЮКЏЪ§ЕФЭМЯѓНЛгкСэвЛЕуCЃЌЧвCЕуЕФКсзјБъЮЊЉ1ЃЌACЃКBC=3ЃК1ЃЎ
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉЩшЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуЮЊFЃЌЦфЖдГЦжсгыжБЯпABМАxжсЗжБ№НЛгкЕуDКЭЕуEЃЌШєЁїFCDгыЁїAEDЯрЫЦЃЌЧѓДЫЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкУРЛЏаЃдАЕФЛюЖЏжаЃЌФГаЫШЄаЁзщЯыНшжњШчЭМЫљЪОЕФжБНЧЧННЧЃЈСНБпзуЙЛГЄЃЉЃЌгУ28mГЄЕФРщАЪЮЇГЩвЛИіОиаЮЛЈдАABCDЃЈРщАЪжЛЮЇABЃЌBCСНБпЃЉЃЌЩшAB=xmЃЎШєдкPДІгавЛПУЪїгыЧНCDЃЌADЕФОрРыЗжБ№ЪЧ15mКЭ6mЃЌвЊНЋетПУЪїЮЇдкЛЈдАФкЃЈКЌБпНчЃЌВЛПМТЧЪїЕФДжЯИЃЉЃЌдђЛЈдАУцЛ§SЕФзюДѓжЕЮЊ_____m2ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com