
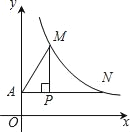
【题目】如图,过点P(2,![]() )作x轴的平行线交y轴于点A,交双曲线
)作x轴的平行线交y轴于点A,交双曲线![]() 于点N,作PM⊥AN交双曲线
于点N,作PM⊥AN交双曲线![]() 于点M,连接AM,若PN=4.
于点M,连接AM,若PN=4.
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式![]() 的解集.
的解集.
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
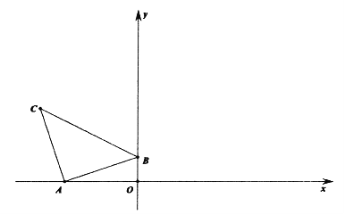
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(-3,0),B(0,1),C(m,n)。
(1)请直接写出C点坐标。
(2)将△ABC 沿x轴的正方向平移t个单位,![]() 、
、![]() 两点的对应点、正好落在反比例函数
两点的对应点、正好落在反比例函数![]() 在第一象限内图象上。请求出t,k的值。
在第一象限内图象上。请求出t,k的值。
(3)在(2)的条件下,问是否存x轴上的点M和反比例函数![]() 图象上的点N,使得以
图象上的点N,使得以![]() 、
、![]() 、M、N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由。
、M、N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司2月份销售新上市一种新型低能耗汽车20辆,由于该型汽车的优越的经济适用性,销量快速上升,4月份该公司销售该型汽车达45辆.
(1)求该公司销售该型汽车3月份和4月份的平均增长率;
(2)该型汽车每辆的进价为10万元;且销售a辆汽车,汽车厂返利销售公司0.03a万元/辆,该公司的该型车售价为11万元/辆,若使5月份每辆车盈利不低于2.6万元,那么该公司5月份至少需要销售该型汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为维护南海主权,我海军舰艇加强对南海海域的巡航,![]() 年
年![]() 月
月![]() 日上午
日上午![]() 时,我海巡
时,我海巡![]() 号舰艇在观察点
号舰艇在观察点![]() 处观测到其正东方向
处观测到其正东方向![]() 海里处有一灯塔
海里处有一灯塔![]() ,该舰艇沿南偏东
,该舰艇沿南偏东![]() 的方向航行,
的方向航行,![]() 时到达观察点
时到达观察点![]() ,测得灯塔
,测得灯塔![]() 位于其北偏西
位于其北偏西![]() 方向,求该舰艇的巡航速度?(结果保留整数)
方向,求该舰艇的巡航速度?(结果保留整数)
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
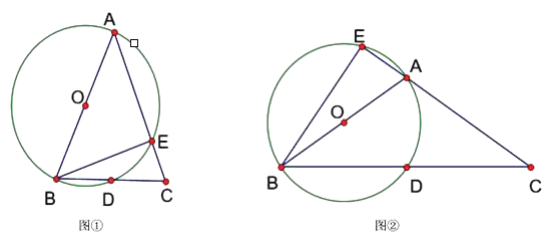
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
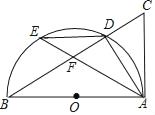
【题目】如图,在Rt△ABC中,∠BAC=90°,以边AB为直径作⊙O,交斜边BC于D,E在弧![]() 上,连接AE、ED、DA,连接AE、ED、DA.
上,连接AE、ED、DA,连接AE、ED、DA.
(1)求证:∠DAC=∠AED;
(2)若点E是![]() 的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com