
【题目】某汽车销售公司2月份销售新上市一种新型低能耗汽车20辆,由于该型汽车的优越的经济适用性,销量快速上升,4月份该公司销售该型汽车达45辆.
(1)求该公司销售该型汽车3月份和4月份的平均增长率;
(2)该型汽车每辆的进价为10万元;且销售a辆汽车,汽车厂返利销售公司0.03a万元/辆,该公司的该型车售价为11万元/辆,若使5月份每辆车盈利不低于2.6万元,那么该公司5月份至少需要销售该型汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
【答案】(1) 该公司销售该型汽车3月份和4月份的平均增长率为50%;(2) 公司5月份至少需要销售该型汽车54辆,此时总盈利至少是141.48万元.
【解析】
(1)设该公司销售该型汽车3月份和4月份的平均增长率为x.等量关系为:2月份的销售量×(1+增长率)2=4月份的销售量,把相关数值代入求解即可.
(2)根据5月份每辆车盈利不低于2.6万元,得到销售汽车辆数的范围,根据整数的性质得到该公司5月份至少需要销售该型汽车多少辆,再根据盈利=销售利润+返利,列出算式即可得到答案.
解:(1)设该公司销售该型汽车3月份和4月份的平均增长率为x,
根据题意列方程:20(1+x)2=45,
解得x1=﹣250%(不合题意,舍去),x2=50%.
答:该公司销售该型汽车3月份和4月份的平均增长率为50%.
(2)由题意得:
0.03a+(11﹣10)≥2.6,
解得:a≥53![]() ,
,
∵a为整数,
∴该公司5月份至少需要销售该型汽车54辆,
(11﹣10)×54+0.03×54×54=141.48(万元).
答:该公司5月份至少需要销售该型汽车54辆,此时总盈利至少是141.48万元.


科目:初中数学 来源: 题型:
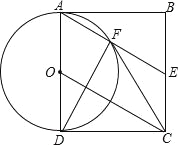
【题目】如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的⊙O与AE交于点F.
(1)求证:四边形AOCE为平行四边形;
(2)求证:CF与⊙O相切;
(3)若F为AE的中点,求∠ADF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
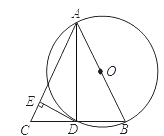
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
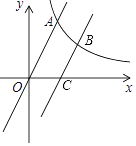
【题目】如图,反比例函数y=![]() (x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
(1)求k的值;
(2)点B为此反比例函数图象上一点,其纵坐标为3.过点B作CB∥OA,交x轴于点C,直接写出线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为![]() 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
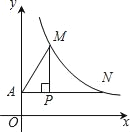
【题目】如图,过点P(2,![]() )作x轴的平行线交y轴于点A,交双曲线
)作x轴的平行线交y轴于点A,交双曲线![]() 于点N,作PM⊥AN交双曲线
于点N,作PM⊥AN交双曲线![]() 于点M,连接AM,若PN=4.
于点M,连接AM,若PN=4.
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两只捕捞船同时在上午![]() 从
从![]() 港出海捕鱼.甲船以
港出海捕鱼.甲船以![]() 的速度沿西偏北
的速度沿西偏北![]() 方向前进,乙船以
方向前进,乙船以![]() 的速度沿东北方向前进.甲船在
的速度沿东北方向前进.甲船在![]() 航行到达
航行到达![]() 处,此时甲船发现部分渔具丢在乙船上,于是甲船快速(匀速)沿北偏东
处,此时甲船发现部分渔具丢在乙船上,于是甲船快速(匀速)沿北偏东![]() 的方向追赶,结果两船在
的方向追赶,结果两船在![]() 处相遇.(其他因素不作考虑)
处相遇.(其他因素不作考虑)
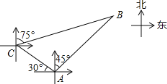
![]() 问乙船在什么时候被甲船追上;
问乙船在什么时候被甲船追上;
![]() 求甲船追赶乙船的速度.
求甲船追赶乙船的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为________;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块含30°角的三角板的直角顶点放在反比例函数y=﹣![]() (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标坐标为_____.
(x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标坐标为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com