
 如图,细心观察图形,认真分析各式,然后再解答问题.${(\sqrt{1})}^{2}$+1=2,S1=$\frac{\sqrt{1}}{2}$${(\sqrt{2})}^{2}$+1=3,S2=$\frac{\sqrt{2}}{2}$${(\sqrt{2})}^{2}$+1=4,S3=$\frac{\sqrt{3}}{2}$
如图,细心观察图形,认真分析各式,然后再解答问题.${(\sqrt{1})}^{2}$+1=2,S1=$\frac{\sqrt{1}}{2}$${(\sqrt{2})}^{2}$+1=3,S2=$\frac{\sqrt{2}}{2}$${(\sqrt{2})}^{2}$+1=4,S3=$\frac{\sqrt{3}}{2}$分析 (1)此题要利用直角三角形的面积公式,观察上述结论,会发现,第n个图形的一直角边就是$\sqrt{n}$,然后利用面积公式可得.
(2)由同述OA2=$\sqrt{2}$,0A3=$\sqrt{3}$…可知OA10=$\sqrt{10}$.
(3)S12+S22+S32+…+S102的值就是把面积的平方相加就可.
解答 解:(1)依题意得:($\sqrt{n}$)2+1=n+1,Sn=$\frac{\sqrt{n}}{2}$.
故答案是:${(\sqrt{n})^2}+1=n+1,{S_n}=\frac{{\sqrt{n}}}{2}$;
(2))∵OA1=$\sqrt{1}$,OA2=$\sqrt{2}$,OA3=$\sqrt{3}$,…
∴OA10=$\sqrt{10}$.
故答案是:$\sqrt{10}$;
(3)S12+S22+S32+…+S102
=($\frac{\sqrt{1}}{2}$)2+($\frac{\sqrt{2}}{2}$)2+($\frac{\sqrt{3}}{2}$)2+…+($\frac{\sqrt{10}}{2}$)2,
=$\frac{1}{4}$(1+2+3+…+10)
=$\frac{55}{4}$.
点评 本题考查了勾股定理.此题的关键是观察,观察题中给出的结论,由此结论找出规律进行计算.千万不可盲目计算.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
 在学习了三角形的相关知识后,老师给小梅留了道作业题,请你帮小梅做完这道题.
在学习了三角形的相关知识后,老师给小梅留了道作业题,请你帮小梅做完这道题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>3 | B. | m≥3 | C. | m<3 | D. | m≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{1.2}$ | D. | $\sqrt{-|x|-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
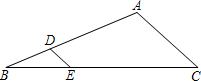 如图,在△ABC中,DE∥AC,$\frac{BD}{DA}=\frac{1}{2}$,DE=3,则AC的长为( )
如图,在△ABC中,DE∥AC,$\frac{BD}{DA}=\frac{1}{2}$,DE=3,则AC的长为( )| A. | 3 | B. | 4 | C. | 6 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com