
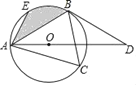
【题目】如图,已知:△ABC的外接圆⊙O的圆心O在等腰△ABD的底边AD上,点E为弧AB上的一点,AB平分∠EAD,∠C=60°,AB=BD=3.
(1)求证:BD是⊙O的切线;
(2)求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
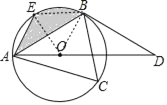
(1)连接OB,根据圆的基本性质,证OB⊥BD,即可得BD是⊙O的切线;(2)连接OE、BE,在Rt△OBD中,∠D=30°,BD=3,得OB=![]() ,证E,B是半圆周的三等分点,得EB∥AO,证得S△ABE=S△OBE,根据S阴影=S扇形OEB可得.
,证E,B是半圆周的三等分点,得EB∥AO,证得S△ABE=S△OBE,根据S阴影=S扇形OEB可得.
(1)证明:连接OB,
∵∠C=60°,
∴∠AOB=2∠C=120°,
∵OA=OB,
∴∠BAO=∠ABO=30°,
∴AB=BD,
∠BAO=∠D=30°,
∴∠ABD=180°﹣∠BAO﹣∠D=120°,
∴∠OBD=∠ABD﹣∠ABO=120°﹣30°=90°,
即OB⊥BD,
∴BD是⊙O的切线;
(2)连接OE、BE,
在Rt△OBD中,∠D=30°,BD=3,
∴OB=![]() ,
,
∵AB平分∠EAD,
∴∠EAB=∠BAO=30°,
∴∠EOB=∠BOD=60°,
∴E,B是半圆周的三等分点,
又∵OE=OB,
∴△OBE是等边三角形,
∴∠OEB=∠AOE=60°,
∴EB∥AO,
∴S△ABE=S△OBE,
∴S阴影=S扇形OEB=![]() .
.


科目:初中数学 来源: 题型:
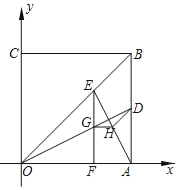
【题目】如图,正方形OABC的顶点O与原点重合,点A,C分别在x轴与y轴的正半轴上,点A的坐标为(4,0),点D在边AB上,且tan∠AOD=![]() ,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H.
,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H.
(1)求B,D两点的坐标;
(2)当点E在线段OB上运动时,求∠HDA的大小;
(3)以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
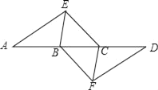
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC
(1)求证:四边形BFCE是平行四边形;
(2)如果AD=5,DC=![]() ,∠EBD=60°,那么当四边形BFCE为菱形时BE的长是多少?
,∠EBD=60°,那么当四边形BFCE为菱形时BE的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级学生的数学作业完成情况,将完成情况分为四个等级:
等级 | A | B | C | D |
情况分类 | 好 | 较好 | 一般 | 不好 |
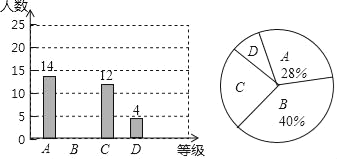
随机对该年级若干名学生进行了调查,然后把调查结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:
(1)补全条形统计图;
(2)该年级共有700人,估计该年级数学作业完成等级为D等的人数;
(3)在此次调查中,有甲、乙、丙、丁四个班的学生数学作业完成表现出色,现决定从这四个班中随机选取两个班在全校举行一次数学作业展览,请用画树状图或列表的方法,求恰好选到甲、乙两个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O作EF∥BC,EF与AB、CD分别相交于点E、F,则△DOF的面积与△BOA的面积之比为( )
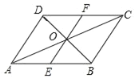
A. 1:2B. 1:4C. 1:8D. 1:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级学生学习《从数据谈节水》后,积极响应“节约用水,从我做起”的号召,下列是10名学生统计各自家族一个月的节水情况:
节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
家族数(个) | 1 | 2 | 2 | 4 | 1 |
那么这组数据的众数和中位数分别是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
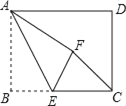
【题目】矩形纸片ABCD中(如图),已知AB=6,BC=8,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC.当△EFC为直角三角形时,线段BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
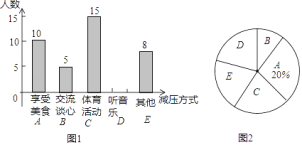
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com