
【题目】如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O作EF∥BC,EF与AB、CD分别相交于点E、F,则△DOF的面积与△BOA的面积之比为( )
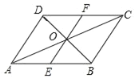
A. 1:2B. 1:4C. 1:8D. 1:16
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动:同时点Q沿边AB,BC从点A开始向点C以acm/s的速度移动,当点P移动到点A时,P,Q同时停止移动.设点P出发x秒时,△PAQ的面积为ycm2,y与x的函数图象如图②,线段EF所在的直线对应的函数关系式为y=﹣4x+21,则a的值为( )
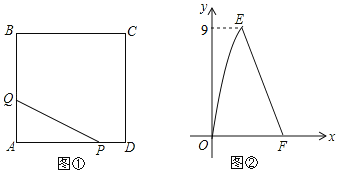
A. 1.5B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
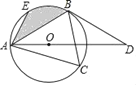
【题目】如图,已知:△ABC的外接圆⊙O的圆心O在等腰△ABD的底边AD上,点E为弧AB上的一点,AB平分∠EAD,∠C=60°,AB=BD=3.
(1)求证:BD是⊙O的切线;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
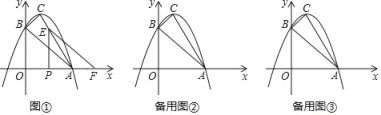
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0).与y轴的交点为B(0,3),其顶点为C.
(1)求抛物线的解析式;
(2)将△AOB沿x轴向右平移m个长度单位(0<m<3)后得到另一个△FPE,点A、O、B的像分别为点F、P、E.
①如图①,当点E在直线AC上时,求m的值.
②设所得的三角形△FPE与△ABC重叠部分的面积为S,求S关于m的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正△ABC中,点D为BC边的中点,将∠ACB绕点C顺时针旋转α角度(0°<α<60°)得∠A'CB',点P为线段A′C上的一点,连接PD与B′C、AC分别交点点E、F,且∠PAC=∠EDC.
(1)求证:AP=2ED;
(2)猜想PA和PC的位置关系,并说明理由;
(3)如图2,连接AD交B'C于点G,若AP=2,PC=4,求AG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假期里,小华和小亮到某影城看电影,影城同时在四个放映室(1、2、3、4室)播放四部不同的电影,他们各自在这四个放映室任选一个,每个放映室被选中的可能性都相同.
(1)小明选择“1室”的概率为 (直接填空)
(2)用树状图或列表的方法求小华和小亮选择去同一间放映室看电影的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com