【题目】假期里，小华和小亮到某影城看电影，影城同时在四个放映室（1、2、3、4室）播放四部不同的电影，他们各自在这四个放映室任选一个，每个放映室被选中的可能性都相同．
（1）小明选择“1室”的概率为 （直接填空）
（2）用树状图或列表的方法求小华和小亮选择去同一间放映室看电影的概率．
科目：初中数学 来源： 题型：
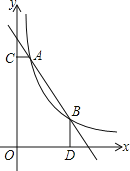
【题目】如图，一次函数
与函数
的图象交于
，
两点，
轴于C，
轴于D
求k的值；
根据图象直接写出
的x的取值范围；
是线段AB上的一点，连接PC，PD，若
和
面积相等，求点P坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
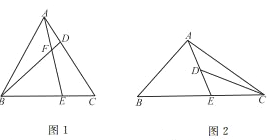
【题目】如图1，在△ABC中，D，E分别是AC，BC边上的点，且AD=CE，连接BD，AE相交于点F。
（1）当∠ABC=∠C=60°时，
，那么
；（直接写出结论）
（2）当△ABC为等边三角形，
时，请用含n的式子表示AF，BF的数量关系，并说明理由；
（3）如图2，在△ABC中，∠ABC=45°，∠ACB=30°，AC=
，点E在BC上，点D是AE的中点，当∠EDC=30°时，CE和DE的数量关系为。（直接写出结论，不必证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
中， 
， 
， 
，D是AB边的中点，E是AC边上一点，联结DE，过点D作
交BC边于点F，联结EF．
（1）如图1，当
时，求EF的长；
（2）如图2，当点E在AC边上移动时， 
的正切值是否会发生变化，如果变化请说出变化情况；如果保持不变，请求出
的正切值；
（3）如图3，联结CD交EF于点Q，当
是等腰三角形时，请直接写出BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
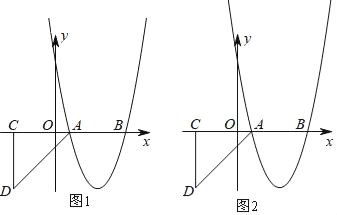
【题目】如图，抛物线y＝x2+bx+c与x轴分别交于A（1，0），B（5，0）两点．
（1）求抛物线的解析式；
（2）过C（﹣3，0）向x轴下方作CD垂直x轴，连接AD，已知CD＝4，将Rt△ACD沿x轴向右平移m个单位，当点D落在抛物线上时，求m的值；
（3）在（2）的条件下，当点D第一次落在抛物线上记为点E，点P是抛物线对称轴上一点，试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx﹣3a经过点A（﹣1，0）、C（0，3），与x轴交于另一点B，抛物线的顶点为D．
（1）求此二次函数解析式；
（2）连接DC、BC、DB，求证：△BCD是直角三角形；
（3）在对称轴右侧的抛物线上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y=
（k≠0，x＞0）的图象同时经过顶点C，D．若点C的横坐标为5，BE=3DE，则k的值为（ ）
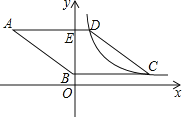
A. 
B. 3 C. 
D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
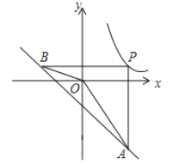
【题目】如图，P为反比例函数
（k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y=﹣x﹣2的图象于点A、B．若∠AOB=135°，则k的值是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
