
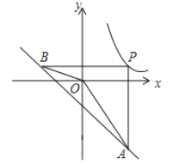
【题目】如图,P为反比例函数![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣2的图象于点A、B.若∠AOB=135°,则k的值是________.
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣2的图象于点A、B.若∠AOB=135°,则k的值是________.
【答案】2
【解析】
作BF⊥x轴,OE⊥AB,CQ⊥AP,易证△BOE∽△AOD,根据相似三角形对应边比例相等的性质即可求出k的值.
作BF⊥x轴,OE⊥AB,CQ⊥AP,如图,

设P点坐标(n,![]() ),
),
∵直线AB函数式为y=-x-2,PB⊥y轴,PA⊥x轴,
∴C(0,-2),G(-2,0),
∴OC=OG,
∴∠OGC=∠OCG=45°
∵PB∥OG,PA∥OC,
∴∠PBA=∠OGC=45°,∠PAB=∠OCG=45°,
∴PA=PB,
∵P点坐标(n,![]() ),
),
∴OD=CQ=n,
∴AD=AQ+DQ=n+2;
∵当x=0时,y=-x-2=-2,
∴OC=DQ=2,GE=OE=![]() OC=
OC=![]() ;
;
同理可证:BG=![]() BF=
BF=![]() PD=
PD=![]() ,
,
∴BE=BG+EG=![]() +
+![]() ;
;
∵∠AOB=135°,
∴∠OBE+∠OAE=45°,
∵∠DAO+∠OAE=45°,
∴∠DAO=∠OBE,
∵在△BOE和△AOD中,
![]() ,
,
∴△BOE∽△AOD;
∴![]() ,即
,即![]() ;
;
解得:k=2;
故选A.


科目:初中数学 来源: 题型:
【题目】假期里,小华和小亮到某影城看电影,影城同时在四个放映室(1、2、3、4室)播放四部不同的电影,他们各自在这四个放映室任选一个,每个放映室被选中的可能性都相同.
(1)小明选择“1室”的概率为 (直接填空)
(2)用树状图或列表的方法求小华和小亮选择去同一间放映室看电影的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量白塔的高度AB,在D处用高为1.5米的测角仪 CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB.(参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数)
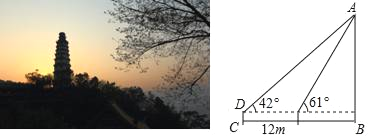
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行了“校园好声音”演唱比赛活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.

根据图中提供的信息,回答下列问题:
(1)求参加演唱比赛的学生共有多少人,并把条形图补充完整;
(2)求出扇形统计图中,m= ,n= ;
(3)求出C等级对应扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)如图1,将△DEC沿射线EC方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.
(2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
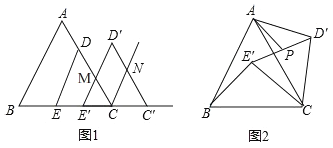
查看答案和解析>>
科目:初中数学 来源: 题型:
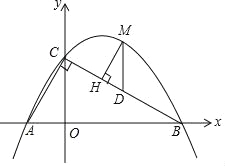
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饭店推出一种早点套餐,试销一段时间后发现,每份套餐的成本为5元,若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份,该店每天固定支出费用为600元![]() 不含套餐成本
不含套餐成本![]() 为了便于结算,每份套餐的售价取整数,设每份套餐的售价为
为了便于结算,每份套餐的售价取整数,设每份套餐的售价为![]() 元,该店日销售利润为y元
元,该店日销售利润为y元![]() 日销售利润
日销售利润![]() 每天的销售额
每天的销售额![]() 套餐成本
套餐成本![]() 每天固定支出
每天固定支出![]()
![]() 求y与x的函数关系式并写出自变量的取值范围.
求y与x的函数关系式并写出自变量的取值范围.
![]() 该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com