
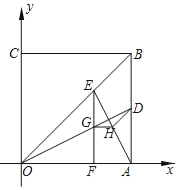
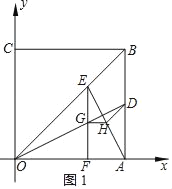
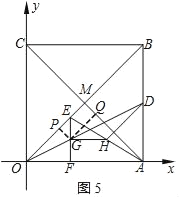
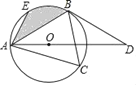
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOABCЕФЖЅЕуOгыдЕужиКЯЃЌЕуAЃЌCЗжБ№дкxжсгыyжсЕФе§АыжсЩЯЃЌЕуAЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЌЕуDдкБпABЩЯЃЌЧвtanЁЯAODЃН![]() ЃЌЕуEЪЧЩфЯпOBЩЯвЛЖЏЕуЃЌEFЁЭxжсгкЕуFЃЌНЛЩфЯпODгкЕуGЃЌЙ§ЕуGзїGHЁЮxжсНЛAEгкЕуHЃЎ
ЃЌЕуEЪЧЩфЯпOBЩЯвЛЖЏЕуЃЌEFЁЭxжсгкЕуFЃЌНЛЩфЯпODгкЕуGЃЌЙ§ЕуGзїGHЁЮxжсНЛAEгкЕуHЃЎ
ЃЈ1ЃЉЧѓBЃЌDСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЕБЕуEдкЯпЖЮOBЩЯдЫЖЏЪБЃЌЧѓЁЯHDAЕФДѓаЁЃЛ
ЃЈ3ЃЉвдЕуGЮЊдВаФЃЌGHЕФГЄЮЊАыОЖЛЁбGЃЎЪЧЗёДцдкЕуEЪЙЁбGгые§ЗНаЮOABCЕФЖдНЧЯпЫљдкЕФжБЯпЯрЧаЃПШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФЕуEЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЈ4ЃЌ4ЃЉЃЌDЃЈ4ЃЌ2ЃЉЃЛЃЈ2ЃЉ45ЁуЃЛЃЈ3ЃЉДцдкЃЌЗћКЯЬѕМўЕФЕуЮЊЃЈ8Љ4![]() ЃЌ8Љ4
ЃЌ8Љ4![]() ЃЉЛђЃЈ8+4
ЃЉЛђЃЈ8+4![]() ЃЌ8+4
ЃЌ8+4![]() ЃЉЛђ
ЃЉЛђ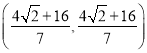 Лђ
Лђ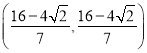 ЃЌРэгЩМћНтЮі
ЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉгЩе§ЗНаЮаджЪжЊAB=OA=4ЃЌЁЯOAB=90ЁуЃЌОнДЫЕУBЃЈ4ЃЌ4ЃЉЃЌдйгЩtanЁЯAOD= ![]() ЕУAD=
ЕУAD=![]() OA=2ЃЌОнДЫПЩЕУЕуDзјБъЃЛ
OA=2ЃЌОнДЫПЩЕУЕуDзјБъЃЛ
ЃЈ2ЃЉгЩ![]() жЊGF=
жЊGF=![]() OFЃЌдйгЩЁЯAOB=ЁЯABO=45ЁужЊOF=EFЃЌМДGF=
OFЃЌдйгЩЁЯAOB=ЁЯABO=45ЁужЊOF=EFЃЌМДGF=![]() EFЃЌИљОнGHЁЮxжсжЊHЮЊAEЕФжаЕуЃЌНсКЯDЮЊABЕФжаЕужЊDHЪЧЁїABEЕФжаЮЛЯпЃЌМДHDЁЮBEЃЌОнДЫПЩЕУД№АИЃЛ
EFЃЌИљОнGHЁЮxжсжЊHЮЊAEЕФжаЕуЃЌНсКЯDЮЊABЕФжаЕужЊDHЪЧЁїABEЕФжаЮЛЯпЃЌМДHDЁЮBEЃЌОнДЫПЩЕУД№АИЃЛ
ЃЈ3ЃЉЗжЁбGгыЖдНЧЯпOBКЭЖдНЧЯпACЯрЧаСНжжЧщПіЃЌЩшPG=xЃЌНсКЯЬтвтНЈСЂЙигкxЕФЗНГЬЧѓНтПЩЕУЃЎ
НтЃКЃЈ1ЃЉЁпAЃЈ4ЃЌ0ЃЉЃЌ
ЁрOAЃН4ЃЌ
ЁпЫФБпаЮOABCЮЊе§ЗНаЮЃЌ
ЁрABЃНOAЃН4ЃЌЁЯOABЃН90ЁуЃЌ
ЁрBЃЈ4ЃЌ4ЃЉЃЌ
дкRtЁїOADжаЃЌЁЯOADЃН90ЁуЃЌ
ЁпtanЁЯAODЃН![]() ЃЌ
ЃЌ
ЁрADЃН![]() OAЃН
OAЃН![]() ЁС4ЃН2ЃЌ
ЁС4ЃН2ЃЌ
ЁрDЃЈ4ЃЌ2ЃЉЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌдкRtЁїOFGжаЃЌЁЯOFGЃН90Ёу
ЁрtanЁЯGOFЃН![]() ЃН
ЃН![]() ЃЌМДGFЃН
ЃЌМДGFЃН![]() OFЃЌ
OFЃЌ
ЁпЫФБпаЮOABCЮЊе§ЗНаЮЃЌ
ЁрЁЯAOBЃНЁЯABOЃН45ЁуЃЌ
ЁрOFЃНEFЃЌ
ЁрGFЃН![]() EFЃЌ
EFЃЌ
ЁрGЮЊEFЕФжаЕуЃЌ
ЁпGHЁЮxжсНЛAEгкHЃЌ
ЁрHЮЊAEЕФжаЕуЃЌ
ЁпBЃЈ4ЃЌ4ЃЉЃЌDЃЈ4ЃЌ2ЃЉЃЌ
ЁрDЮЊABЕФжаЕуЃЌ
ЁрDHЪЧЁїABEЕФжаЮЛЯпЃЌ
ЁрHDЁЮBEЃЌ
ЁрЁЯHDAЃНЁЯABOЃН45ЁуЃЎ
ЃЈ3ЃЉЂйШєЁбGгыЖдНЧЯпOBЯрЧаЃЌ
ШчЭМ2ЃЌЕБЕуEдкЯпЖЮOBЩЯЪБЃЌ
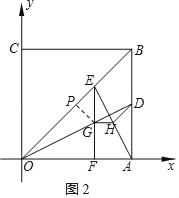
Й§ЕуGзїGPЁЭOBгкЕуPЃЌЩшPGЃНxЃЌПЩЕУPEЃНxЃЌEGЃНFGЃН![]() xЃЌ
xЃЌ
OFЃНEFЃН2![]() xЃЌ
xЃЌ
ЁпOAЃН4ЃЌ
ЁрAFЃН4Љ2![]() xЃЌ
xЃЌ
ЁпGЮЊEFЕФжаЕуЃЌHЮЊAEЕФжаЕуЃЌ
ЁрGHЮЊЁїAFEЕФжаЮЛЯпЃЌ
ЁрGHЃН![]() AFЃН
AFЃН![]() ЁСЃЈ4Љ2
ЁСЃЈ4Љ2![]() xЃЉЃН2Љ
xЃЉЃН2Љ![]() xЃЌ
xЃЌ
дђxЃН2Љ![]() xЃЌ
xЃЌ
НтЕУЃКxЃН2![]() Љ2ЃЌ
Љ2ЃЌ
ЁрEЃЈ8Љ4![]() ЃЌ8Љ4
ЃЌ8Љ4![]() ЃЉЃЌ
ЃЉЃЌ
ШчЭМ3ЃЌЕБЕуEдкЯпЖЮOBЕФбгГЄЯпЩЯЪБЃЌ
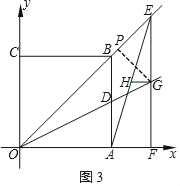
xЃН![]() xЉ2ЃЌ
xЉ2ЃЌ
НтЕУЃКxЃН2+![]() ЃЌ
ЃЌ
ЁрEЃЈ8+4![]() ЃЌ8+4
ЃЌ8+4![]() ЃЉЃЛ
ЃЉЃЛ
ЂкШєЁбGгыЖдНЧЯпACЯрЧаЃЌ
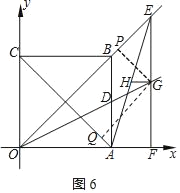
ШчЭМ4ЃЌЕБЕуEдкЯпЖЮBMЩЯЪБЃЌЖдНЧЯпACЃЌOBЯрНЛгкЕуMЃЌ
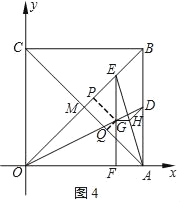
Й§ЕуGзїGPЁЭOBгкЕуPЃЌЩшPGЃНxЃЌПЩЕУPEЃНxЃЌ
EGЃНFGЃН![]() xЃЌ
xЃЌ
OFЃНEFЃН2![]() xЃЌ
xЃЌ
ЁпOAЃН4ЃЌ
ЁрAFЃН4Љ2![]() xЃЌ
xЃЌ
ЁпGЮЊEFЕФжаЕуЃЌHЮЊAEЕФжаЕуЃЌ
ЁрGHЮЊЁїAFEЕФжаЮЛЯпЃЌ
ЁрGHЃН![]() AFЃН
AFЃН![]() ЁСЃЈ4Љ2
ЁСЃЈ4Љ2![]() xЃЉЃН2Љ
xЃЉЃН2Љ![]() xЃЌ
xЃЌ
Й§ЕуGзїGQЁЭACгкЕуQЃЌдђGQЃНPMЃН3xЉ2![]() ЃЌ
ЃЌ
Ёр3xЉ2![]() ЃН2Љ
ЃН2Љ![]() xЃЌ
xЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр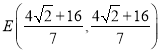 ЃЛ
ЃЛ
ШчЭМ5ЃЌЕБЕуEдкЯпЖЮOMЩЯЪБЃЌ
GQЃНPMЃН2![]() Љ3xЃЌдђ2
Љ3xЃЌдђ2![]() Љ3xЃН2Љ
Љ3xЃН2Љ![]() xЃЌ
xЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёр ЃЛ
ЃЛ
ШчЭМ6ЃЌЕБЕуEдкЯпЖЮOBЕФбгГЄЯпЩЯЪБЃЌ
3xЉ2![]() ЃН
ЃН![]() xЉ2ЃЌ
xЉ2ЃЌ
НтЕУЃК![]() ЃЈЩсШЅЃЉЃЛ
ЃЈЩсШЅЃЉЃЛ
злЩЯЫљЪіЃЌЗћКЯЬѕМўЕФЕуЮЊЃЈ8Љ4![]() ЃЌ8Љ4
ЃЌ8Љ4![]() ЃЉЛђЃЈ8+4
ЃЉЛђЃЈ8+4![]() ЃЌ8+4
ЃЌ8+4![]() ЃЉЛђ
ЃЉЛђ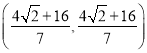 Лђ
Лђ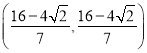 ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпy1ЃНax2+bОЙ§CЃЈЉ2ЃЌ4ЃЉЃЌDЃЈЉ4ЃЌ4ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпy1ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉНЋХзЮяЯпy1биxжсЗелЃЌдйЯђгвЦНвЦЃЌЕУЕНХзЮяЯпy2ЃЌгыy2жсНЛгкЕуFЃЌЕуEЮЊХзЮяЯп2ЩЯвЛЕуЃЌвЊЪЙвдCDЮЊБпЃЌCЁЂDЁЂEЁЂFЫФЕуЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЧѓЫљгаТњзуЬѕМўЕФХзЮяЯпy2ЕФКЏБэДяЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЃЈ-2ЃЌmЃЉШЦзјБъдЕуOЫГЪБеыа§зЊ90ЁуКѓЃЌЧЁКУТфдкЭМжаЁбPжаЕФвѕгАЧјгђЃЈАќРЈБпНчЃЉФкЃЌЁбPЕФАыОЖЮЊ1ЃЌЕуPЕФзјБъЮЊЃЈ3ЃЌ2ЃЉЃЌдђmЕФШЁжЕЗЖЮЇЪЧ______ЃЎ
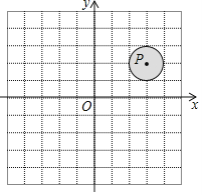
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃПЊеЙвдЫижЪЬсЩ§ЮЊжїЬтЕФбабЇЛюЖЏЃЌЭЦГіСЫвдЯТЫФИіЯюФПЙЉбЇЩњбЁдёЃКAЃЎФЃФтМнЪЛЃЛBЃЎОќЪТОКММЃЛCЃЎМвЯчЕМгЮЃЛDЃЎжВЮяЪЖБ№ЃЎбЇаЃЙцЖЈЃКУПИібЇЩњЖМБиаыБЈУћЧвжЛФмбЁдёЦфжавЛИіЯюФПЃЎАЫФъМЖЃЈ3ЃЉАрАржїШЮСѕРЯЪІЖдШЋАрбЇЩњбЁдёЕФЯюФПЧщПіНјааСЫЭГМЦЃЌВЂЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыНсКЯЭГМЦЭМжаЕФаХЯЂЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉАЫФъМЖЃЈ3ЃЉАрбЇЩњзмШЫЪ§ЪЧЁЁ ЁЁЃЌВЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉСѕРЯЪІЗЂЯжБЈУћВЮМгЁАжВЮяЪЖБ№ЁБЕФбЇЩњжаЧЁКУгаСНУћФаЩњЃЌЯжзМБИДгетаЉбЇЩњжаШЮвтЬєбЁСНУћЕЃШЮЛюЖЏМЧТМдБЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓЧЁКУбЁжа1УћФаЩњКЭ1УћХЎЩњЕЃШЮЛюЖЏМЧТМдБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮЊСЫВтСПНЈжўЮяACЕФИпЖШЃЌДгОрРыНЈжўЮяЕзВПCДІ50УзЕФЕуDЃЈЕуDгыНЈжўЮяЕзВПCдкЭЌвЛЫЎЦНУцЩЯЃЉГіЗЂЃЌбиЦТЖШiЃН1ЃК2ЕФаБЦТDBЧАНј10![]() УзЕНДяЕуBЃЌдкЕуBДІВтЕУНЈжўЮяЖЅВПAЕФбіНЧЮЊ53ЁуЃЌЧѓНЈжўЮяACЕФИпЖШЃЎЃЈНсЙћОЋШЗЕН0.1УзЃЎВЮПМЪ§ОнЃКsin53ЁуЁж0.798ЃЌcos53ЁуЁж0.602ЃЌtan53ЁуЁж1.327ЃЎЃЉ
УзЕНДяЕуBЃЌдкЕуBДІВтЕУНЈжўЮяЖЅВПAЕФбіНЧЮЊ53ЁуЃЌЧѓНЈжўЮяACЕФИпЖШЃЎЃЈНсЙћОЋШЗЕН0.1УзЃЎВЮПМЪ§ОнЃКsin53ЁуЁж0.798ЃЌcos53ЁуЁж0.602ЃЌtan53ЁуЁж1.327ЃЎЃЉ
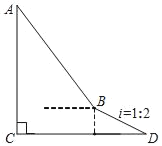
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
ШчЭМ1ЃЌдкЁїOABКЭЁїOCDжаЃЌOA=OBЃЌOC=ODЃЌЁЯAOB=ЁЯCOD=40ЁуЃЌСЌНгACЃЌBDНЛгкЕуMЃЎЬюПеЃК
Ђй![]() ЕФжЕЮЊЁЁ ЁЁЃЛ
ЕФжЕЮЊЁЁ ЁЁЃЛ
ЂкЁЯAMBЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌдкЁїOABКЭЁїOCDжаЃЌЁЯAOB=ЁЯCOD=90ЁуЃЌЁЯOAB=ЁЯOCD=30ЁуЃЌСЌНгACНЛBDЕФбгГЄЯпгкЕуMЃЎЧыХаЖЯ![]() ЕФжЕМАЁЯAMBЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЛ
ЕФжЕМАЁЯAMBЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙбгЩь
дкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЁїOCDШЦЕуOдкЦНУцФка§зЊЃЌACЃЌBDЫљдкжБЯпНЛгкЕуMЃЌШєOD=1ЃЌOB=![]() ЃЌЧыжБНгаДГіЕБЕуCгыЕуMжиКЯЪБACЕФГЄЃЎ
ЃЌЧыжБНгаДГіЕБЕуCгыЕуMжиКЯЪБACЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭўРіЩЬГЁЯњЪлAЁЂBСНжжЩЬЦЗЃЌЪлГі1МўAжжЩЬЦЗКЭ4МўBжжЩЬЦЗЫљЕУРћШѓЮЊ600дЊЃЛЪлГі3МўAжжЩЬЦЗКЭ5МўBжжЩЬЦЗЫљЕУРћШѓЮЊ1100дЊ.
(1)ЧѓУПМўAжжЩЬЦЗКЭУПМўBжжЩЬЦЗЪлГіКѓЫљЕУРћШѓЗжБ№ЮЊЖрЩйдЊЃП
(2)гЩгкашЧѓСПДѓЃЌAЁЂBСНжжЩЬЦЗКмПьЪлЭъЃЌЭўРіЩЬГЁОіЖЈдйвЛДЮЙКНјAЁЂBСНжжЩЬЦЗЙВ34МўЃЌШчЙћНЋет34МўЩЬЦЗШЋВПЪлЭъКѓЫљЕУРћШѓВЛЕЭгк4000дЊЃЌФЧУДЭўРіЩЬГЁжСЩйашЙКНјЖрЩйМўAжжЩЬЦЗЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫСЫНтбЇЩњЕФАВШЋвтЪЖЃЌдкШЋаЃЗЖЮЇФкЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЎИљОнЕїВщНсЙћЃЌАббЇЩњЕФАВШЋвтЪЖЗжГЩЁАЕБЁЁБЁЂЁАвЛАуЁБЁЂЁАНЯЧПЁБЁЂЁАКмЧПЁБЫФИіВуДЮЃЌВЂЛцжЦГЩШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЎ
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮЕїВщвЛЙВГщШЁСЫЁЁ ЁЁУћбЇЩњЃЌНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЃЌЁАНЯЧПЁБВуДЮЫљеМдВаФНЧЕФДѓаЁЮЊЁЁ ЁЁЁуЃЛ
ЃЈ3ЃЉШєИУаЃга1800УћбЇЩњЃЌЯжвЊЖдАВШЋвтЪЖЮЊЁАЕБЁЁБЁЂЁАвЛАуЁБЕФбЇЩњЧПЛЏАВШЋНЬг§ЃЌИљОнЕїВщНсЙћЃЌЧыФуЙРМЦШЋаЃашвЊЧПЛЏАВШЋНЬг§ЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКЁїABCЕФЭтНгдВЁбOЕФдВаФOдкЕШбќЁїABDЕФЕзБпADЩЯЃЌЕуEЮЊЛЁABЩЯЕФвЛЕуЃЌABЦНЗжЁЯEADЃЌЁЯCЃН60ЁуЃЌABЃНBDЃН3ЃЎ
ЃЈ1ЃЉЧѓжЄЃКBDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com