
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.

【答案】(1)![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() )(2)①客车和货车的平均速度分别为
)(2)①客车和货车的平均速度分别为![]() 千米/小时和
千米/小时和![]() 千米/小时.②甲地与
千米/小时.②甲地与![]() 加油站的距离为
加油站的距离为![]() 或
或![]() 千米
千米
【解析】
试题(1)利用时间t与速度v成反比例可以得到反比例函数的解析式;
(2)①由客车的平均速度为每小时v千米,得到货车的平均速度为每小时(v-20)千米,根据一辆客车从甲地出发前往乙地,一辆货车同时从乙地出发前往甲地,3小时后两车相遇列出方程,解方程即可;
②分两种情况进行讨论:当A加油站在甲地和B加油站之间时;当B加油站在甲地和A加油站之间时;都可以根据甲、乙两地间有两个加油站A、B,它们相距200千米列出方程,解方程即可.
试题解析:(1)设函数关系式为v=![]() ,
,
∵t=5,v=120,
∴k=120×5=600,
∴v与t的函数关系式为v=![]() (5≤t≤10);
(5≤t≤10);
(2)①依题意,得
3(v+v-20)=600,
解得v=110,
经检验,v=110符合题意.
当v=110时,v-20=90.
答:客车和货车的平均速度分别为110千米/小时和90千米/小时;
②当A加油站在甲地和B加油站之间时,
110t-(600-90t)=200,
解得t=4,此时110t=110×4=440;
当B加油站在甲地和A加油站之间时,
110t+200+90t=600,
解得t=2,此时110t=110×2=220.
答:甲地与B加油站的距离为220或440千米.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
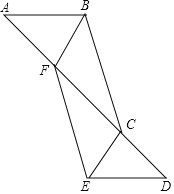
【题目】如图,在△ABC和△DEF中,AB∥DE,点A,F,C,D在同一直线上,AF=CD,∠AFE=∠BCD.
试说明:
(1)△ABC≌△DEF;
(2)BF∥EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
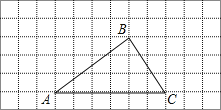
【题目】在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.
(1)过B作AC的平行线BD.
(2)作出表示B到AC的距离的线段BE.
(3)线段BE与BC的大小关系是:BE BC(填“>”、“<”、“=”).
(4)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学家的饮水机中原有水的温度为20 ℃,其工作过程如图所示.在一个由20 ℃加热到100 ℃再降温到20 ℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.
(1)写出水温下降过程中y与x之间的函数表达式,并求出x为何值时,y=100;
(2)求加热过程中y与x之间的函数表达式;
(3)求当x为何值时,y=80.
问题解决
若嘉淇同学上午八点将饮水机通电开机后立刻外出散步,预计九点前回到家中,若嘉淇想喝到不低于50 ℃的水,则直接写出她外出的时间m(分)的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
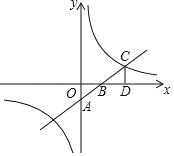
【题目】如图,一次函数 y=kx+b 的图象与坐标轴分别交于 A、B 两点,与反比例函数 y=![]() 的图象在第一象限的交点为点 C,CD⊥x 轴,垂足为点 D,若OB=3,OD=6,△AOB 的面积为 3.
的图象在第一象限的交点为点 C,CD⊥x 轴,垂足为点 D,若OB=3,OD=6,△AOB 的面积为 3.
(1)求一次函数与反比例函数的解析式;
(2)直接写出当 x>0 时,kx+b﹣![]() >0 的解集.
>0 的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且满足
,且满足![]() ,多项式
,多项式![]() 是五次四项式.
是五次四项式.
(1)![]() 的值为 ,
的值为 ,![]() 的值为 ,
的值为 ,![]() 的值为 .
的值为 .
(2)已知点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 以每秒3个单位的速度向右运动,同时点
以每秒3个单位的速度向右运动,同时点![]() 从点
从点![]() 出发,以每秒7个单位的速度向左运动:
出发,以每秒7个单位的速度向左运动:
①若点![]() 从点
从点![]() 出发,点
出发,点![]() 和点
和点![]() 经过
经过![]() 秒后,在数轴上的点
秒后,在数轴上的点![]() 处相遇,求
处相遇,求![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
②若点![]() 先从点
先从点![]() 出发,运动到点
出发,运动到点![]() 处,点
处,点![]() 再出发,则点
再出发,则点![]() 运动几秒后两点之间的距离为5个单位长度?
运动几秒后两点之间的距离为5个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
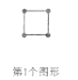
【题目】如图,用小木棒摆成第1个图形所需要的木棒根数是4根,摆成第2个图形所需要的木棒根数是12根,摆成第3个图形所需要的木棒根数是24根……按照此规律摆放,摆成第10个图形所需要的木棒根数是__________根.

 …
…
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们环保意识的增强,越来越多的人选择低碳出行,各种品牌的山地自行车相继投放市场.顺风车行五月份![]() 型车的销售总利润为
型车的销售总利润为![]() 元,
元,![]() 型车的销售总利润为
型车的销售总利润为![]() 元.且
元.且![]() 型车的销售数量是
型车的销售数量是![]() 型车的
型车的![]() 倍,已知销售
倍,已知销售![]() 型车比
型车比![]() 型车每辆可多获利
型车每辆可多获利![]() 元.
元.
(1)求每辆![]() 型车和
型车和![]() 型车的销售利润;
型车的销售利润;
(2)若该车行计划一次购进![]() 两种型号的自行车共
两种型号的自行车共![]() 台且全部售出,其中
台且全部售出,其中![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车的
型车的![]() 倍,则该车行购进
倍,则该车行购进![]() 型车、
型车、![]() 型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,每辆车的月租金为4000元时,可全部租出.每辆车的月租金每增加100元,未租出的车将增加1辆.租出的车每辆每月的维护费为500元,未租出的车每辆每月只需维护费100元.
(1)当每辆车的月租金为4600元时,能租出多少辆?并计算此时租赁公司的月收益(租金收入扣除维护费)是多少万元?
(2)规定每辆车月租金不能超过7200元,当每辆车的月租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达40.4万元?
(3)当每辆车的月租金定为_________元时,租赁公司的月收益最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com