
【题目】嘉淇同学家的饮水机中原有水的温度为20 ℃,其工作过程如图所示.在一个由20 ℃加热到100 ℃再降温到20 ℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.
(1)写出水温下降过程中y与x之间的函数表达式,并求出x为何值时,y=100;
(2)求加热过程中y与x之间的函数表达式;
(3)求当x为何值时,y=80.
问题解决
若嘉淇同学上午八点将饮水机通电开机后立刻外出散步,预计九点前回到家中,若嘉淇想喝到不低于50 ℃的水,则直接写出她外出的时间m(分)的取值范围.

【答案】(1) 8(2) y=10x+20(0≤x<8)(3)当x=6或x=10时,y=80[问题解决]外出时间m(分)的取值范围为3≤m≤16或43≤m≤56.
【解析】(1)根据待定系数法可求饮水机水温的下降过程中y与x的函数关系式,再求出y=100时x的值即可求解;
(2)根据待定系数法可求加热过程中y与x之间的函数关系;
(3)分两种情况:加热过程中;降温过程中;y=80时x的值即可求解;
问题解决:根据一次函数和反比例函数的增减性即可求解.
(1)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为:y=![]() ,
,
依据题意,得:100=![]() ,
,
即m=800,
故y=![]() ,
,
当y=100时,100=![]() ,
,
解得:x=8;
(2)设水温y(℃)与开机时间x(分)的函数关系为:y=kx+b,
依据题意,得![]() ,
,
解得:![]() .
.
故此函数解析式为:y=10x+20;
(3)当y=80时:
加热过程中:10x+20=80,解得x=6;
降温过程中:![]() =80,解得x=10;
=80,解得x=10;
综上所述,x=6或10时,y=80;
问题解决:外出时间m(分钟)的取值范围为3≤m≤16或43≤m≤56.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.
如:①用配方法分解因式:a2+6a+8,
解:原式=a2+6a+8+1﹣1=a2+6a+9﹣1=(a+2)(a+4)
②M=a2﹣2ab+2b2﹣2b+2,利用配方法求M的最小值,
解:a2﹣2ab+2b2﹣2b+2=a2﹣2ab+b2+b2﹣2b+1+1=(a﹣b)2+(b﹣1)2+1
∵(a﹣b)2≥0,(b﹣1)2≥0
∴当a=b=1时,M有最小值1.
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:x2﹣![]() x+ .
x+ .
(2)用配方法因式分解:x2﹣4xy+3y2.
(3)若M=![]() x2+2x﹣1,求M的最小值.
x2+2x﹣1,求M的最小值.
(4)已知x2+2y2+z2﹣2xy﹣2y﹣4z+5=0,则x+y+z的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为( )
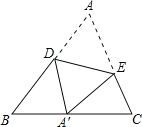
A. 35°B. 40°C. 45°D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
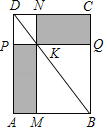
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A,B,C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是________.
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,P为AB边上不与A,B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是______.
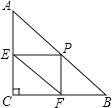
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com