
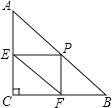
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,P为AB边上不与A,B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是______.
科目:初中数学 来源: 题型:
【题目】嘉淇同学家的饮水机中原有水的温度为20 ℃,其工作过程如图所示.在一个由20 ℃加热到100 ℃再降温到20 ℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.
(1)写出水温下降过程中y与x之间的函数表达式,并求出x为何值时,y=100;
(2)求加热过程中y与x之间的函数表达式;
(3)求当x为何值时,y=80.
问题解决
若嘉淇同学上午八点将饮水机通电开机后立刻外出散步,预计九点前回到家中,若嘉淇想喝到不低于50 ℃的水,则直接写出她外出的时间m(分)的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们环保意识的增强,越来越多的人选择低碳出行,各种品牌的山地自行车相继投放市场.顺风车行五月份![]() 型车的销售总利润为
型车的销售总利润为![]() 元,
元,![]() 型车的销售总利润为
型车的销售总利润为![]() 元.且
元.且![]() 型车的销售数量是
型车的销售数量是![]() 型车的
型车的![]() 倍,已知销售
倍,已知销售![]() 型车比
型车比![]() 型车每辆可多获利
型车每辆可多获利![]() 元.
元.
(1)求每辆![]() 型车和
型车和![]() 型车的销售利润;
型车的销售利润;
(2)若该车行计划一次购进![]() 两种型号的自行车共
两种型号的自行车共![]() 台且全部售出,其中
台且全部售出,其中![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车的
型车的![]() 倍,则该车行购进
倍,则该车行购进![]() 型车、
型车、![]() 型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b为有理数,且a,b不为0,则定义有理数对(a,b)的“真诚值”为d(a,b)= ,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
(1)求有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)求证:有理数对(a,b)与(b,a)的“真诚值”相等;
(3)若(a,2)的“真诚值”的绝对值为|d(a,2)|,若|d(a,2)|=6,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元。
(1)若该起市同时一次购进甲、两种商品共80件,恰好用去1600元,求能购进甲乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80件的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
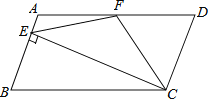
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是______.(把所有正确结论的序号都填在横线上)①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,每辆车的月租金为4000元时,可全部租出.每辆车的月租金每增加100元,未租出的车将增加1辆.租出的车每辆每月的维护费为500元,未租出的车每辆每月只需维护费100元.
(1)当每辆车的月租金为4600元时,能租出多少辆?并计算此时租赁公司的月收益(租金收入扣除维护费)是多少万元?
(2)规定每辆车月租金不能超过7200元,当每辆车的月租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达40.4万元?
(3)当每辆车的月租金定为_________元时,租赁公司的月收益最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
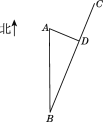
【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com