练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知⊙O和⊙O上的一点A，作⊙O的内接正方形和内接正六边形(点A为正方形和正六边形的顶点)．

    【答案】见解析

    【解析】

    ①作直径AC；

    ②作直径BD⊥AC，依次连接AB，BC，CD，DA，则四边形ABCD是⊙O的内接正方形；

    ③分别以点A，C为圆心，OA的长为半径画弧，交⊙O于点E，H和F，G，顺次连接AE，EF，FC，CG，GH，HA，则六边形AEFCGH为⊙O的内接正六边形．

    作法：①作直径AC；

    ②作直径BD⊥AC，依次连接AB，BC，CD，DA，则四边形ABCD是⊙O的内接正方形；

    ③分别以点A，C为圆心，OA的长为半径画弧，交⊙O于点E，H和F，G，顺次连接AE，EF，FC，CG，GH，HA，则六边形AEFCGH为⊙O的内接正六边形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

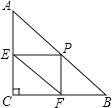
    【题目】如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，P为AB边上不与A，B重合的一动点，过点P分别作PE⊥AC于点E，PF⊥BC于点F，则线段EF的最小值是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某市文化节期间，在景观湖中央搭建了一个舞台C，在岸边搭建了三个看台A，B，D，其中A，C，D三点在同一条直线上，看台A，B到舞台C的距离相等，测得∠A＝30°，∠D＝45°，AB＝60 m，小明、小丽分别在B，D看台观看演出，请分别求出小明、小丽与舞台C的距离．(结果保留根号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某体育用品商店，准备用不超过2800元购买足球和篮球共计60个，已知一个篮球的进价为50元，售价为65元；一个足球的进价为40元，售价为50元.

    （1）若购进x个篮球，购买这批球共花费y元，求y与x之间的函数关系式；

    （2）设售出这批球共盈利w元，求w与x之间的函数关系式；

    （3）体育用品商店购进篮球和足球各多少个时，才能获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若AB是⊙O内接正五边形的一边，AC是⊙O内接正六边形的一边，则∠BAC等于(　　)

    A. 120° B. 6° C. 114° D. 114°或6°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：直线AB与直线CD交于点O，过点O作OE⊥AB．

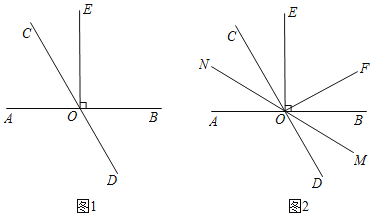
    （1）如图1，∠BOC＝2∠AOC，求∠COE的度数；

    （2）如图2．在（1）的条件下，过点O作OF⊥CD，经过点O画直线MN，满足射线OM平分∠BOD，在不添加任何辅助线的情况下，请直接写出与2∠EOF度数相等的角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A＝90°，AB＝AC，∠ABC的平分线BD交AC于点D，CE⊥BD交BD的延长线于点E，若BD＝2，则CE＝_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

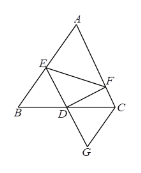
    【题目】如图，在△ABC中，D为BC的中点，E为AB上一点，DF⊥DE交AC于点F，延长ED至点G，使GD＝ED，连接CG．

    (1)求证：BE＝CG；

    (2)求证：BE＋CF＞EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】杨辉是中国南宋末年的一位杰出的数学家，数学教育家．杨辉三角是杨辉的一大重要研究成果，其中蕴含了许多优美的规律．古今中外，许多的数学家都曾对其深入研究过，并将研究结果应用于实践．其中杨辉三角如下

    （1）第5行的数和为________

    （2）观察每行数的和，并归纳出第行数的和为________

    （3）第三斜行的数分别为1，3，6，10，…，请依此规律写出第5个数为 ．请归纳得出第三斜行第个数的表达式________（用含有的表达式表示）

    查看答案和解析>>

    同步练习册答案