
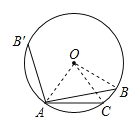
【题目】若AB是⊙O内接正五边形的一边,AC是⊙O内接正六边形的一边,则∠BAC等于( )
A. 120° B. 6° C. 114° D. 114°或6°
【答案】D
【解析】先根据题意画出图形,根据正多边形与圆的关系分别求出中心角∠AOC=60°,∠AOB=72°,再由等边对等角及三角形内角和定理分别求出∠OAC=54°,∠OAB=54°,然后分两种情况进行讨论:①AB、AC都在OA同侧;②AB、AC在OA两侧.
如图,连接OA,OB,OC,
∵AB是⊙O内接正五边形的一边,AC是⊙O的内接正六边形的一边,
∴∠AOC=![]() ,∠AOB=
,∠AOB=![]() =72°,
=72°,
∵OA=OC=OB,
∴∠OAB=54°,∠OAC=60°,
若AB与AC在OA的同侧,∠BAC=∠OAC-∠OAB=6°,
当AB、AC在OA两侧时,则∠BAC=∠OAC+∠OAB=54°+60°=114°.
∴∠BAC=6°或114°.
故选:D


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元。
(1)若该起市同时一次购进甲、两种商品共80件,恰好用去1600元,求能购进甲乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80件的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米处建有一个监测点P,道路AB段为检测区(如图).在△ABP中,已知∠PAB=32°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速?(精确到0.1秒.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.
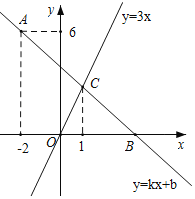
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班去商场为书法比赛买奖品,书包每个定价40元,文具盒每个定价8元,商场实行两种优惠方案:①买一个书包送一个文具盒:②按总价的9折付款.若该班需购买书包10个,购买文具盒若干个(不少于10个).
(1)当买文具盒40个时,分别计算两种方案应付的费用;
(2)当购买文具盒多少个时,两种方案所付的费用相同;
(3)如何根据购买文具盒的个数,选择哪种优惠方案的费用比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
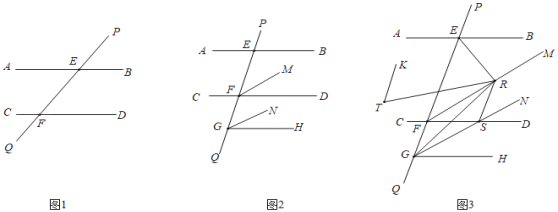
(1)如图1,求证:AB∥CD;
(2)如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;
(3)如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF与六边形A′B′C′D′E′F′相似.
求:(1)相似比;
(2)∠A和∠B′的度数;
(3)边CD,EF,A′F′,E′D′的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com