
【题目】某班去商场为书法比赛买奖品,书包每个定价40元,文具盒每个定价8元,商场实行两种优惠方案:①买一个书包送一个文具盒:②按总价的9折付款.若该班需购买书包10个,购买文具盒若干个(不少于10个).
(1)当买文具盒40个时,分别计算两种方案应付的费用;
(2)当购买文具盒多少个时,两种方案所付的费用相同;
(3)如何根据购买文具盒的个数,选择哪种优惠方案的费用比较合算?
【答案】(1)第①种方案应付的费用为640元,第②种方案应付的费用648元;(2)当购买文具盒50个时,两种方案所付的费用相同;(3)当购买文具盒个数小于50个时,选择方案①比较合算;当购买文具盒个数等于50个时,两种方案所付的费用相同,两种方案都可以选择;当购买文具盒个数大于50个时,选择方案②比较合算.
【解析】
(1)根据商场实行两种优惠方案分别计算即可;
(2)设购买文具盒![]() 个时,两种方案所付的费用相同,由题意得
个时,两种方案所付的费用相同,由题意得![]() ,解方程即可得出结果;
,解方程即可得出结果;
(3)由(1)、(2)可得当购买文具盒个数小于50个时,选择方案①比较合算;当购买文具盒个数等于50个时,两种方案所付的费用相同,两种方案都可以选择;当购买文具盒个数大于50个时,选择方案②比较合算.
解:(1)第①种方案应付的费用为:![]() (元
(元![]() ,
,
第②种方案应付的费用为:![]() (元
(元![]() ;
;
答:第①种方案应付的费用为640元,第②种方案应付的费用648元;
(2)设购买文具盒![]() 个时,两种方案所付的费用相同,
个时,两种方案所付的费用相同,
由题意得:![]() ,
,
解得:![]() ;
;
答:当购买文具盒50个时,两种方案所付的费用相同;
(3)由(1)、(2)可得:当购买文具盒个数小于50个时,选择方案①比较合算;
当购买文具盒个数等于50个时,两种方案所付的费用相同,两种方案都可以选择;
当购买文具盒个数大于50个时,选择方案②比较合算.


科目:初中数学 来源: 题型:
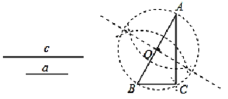
【题目】数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.李明的作法如图所示,作线段AB使AB=C,以AB为直径作⊙O,以B为圆心,a为半径作弧交⊙O于点C,连接AC,△ABC即为所求作的三角形,你认为这种作法中判断∠ACB是直角的依据是( )
A. 90°的圆周角所对的弦是直径 B. 直径所对的圆周角是直角
C. 勾股定理的逆定理 D. 勾股定理
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:

(1)楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生本学期6次数学考试成绩如下表所示:
成绩类别 | 第一次月考 | 第二次月考 | 期中 | 第三次月考 | 第四次月考 | 期末 |
成绩/分 | 105 | 110 | 108 | 113 | 108 | 112 |
(1)6次考试成绩的中位数为 ,众数为 .
(2)求该生本学期四次月考的平均成绩.
(3)如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算,那么该生本学期的数学总评成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种股票第一天的最高价比开盘价高0.3元,最低价比开盘价低0.2元;第二天的最高价开盘价高0.2元,最低价比开盘价低0.1元;第三天的最高价等于开盘价,最低价比开盘价低0.13元.计算每天最高价与最低价的差,以及这些差的平均值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若AB是⊙O内接正五边形的一边,AC是⊙O内接正六边形的一边,则∠BAC等于( )
A. 120° B. 6° C. 114° D. 114°或6°
查看答案和解析>>
科目:初中数学 来源: 题型:
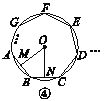
【题目】如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
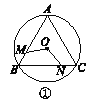
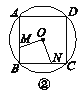
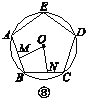
查看答案和解析>>
科目:初中数学 来源: 题型:
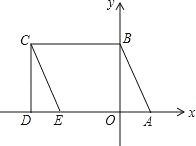
【题目】如图所示,A(2,0),点 B 在 y 轴上,将三角形 OAB 沿 x 轴负方向平移,平移后的图形为三角形 DEC,且点 C 的坐标为(-6,4) .
(1)直接写出点 E 的坐标 ;
(2)在四边形 ABCD 中,点 P 从点 B 出发,沿“BC→CD”移动.若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒,回答下列问题:
①求点 P 在运动过程中的坐标,(用含 t 的式子表示,写出过程);
②当 3 秒<t<5 秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z 之间的数量关系能否确定?若能,请用含 x,y 的式子表示 z,写出过程;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
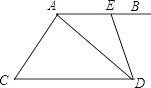
(1)求证:AD平分∠CDE;
(2)若AC⊥AD,∠ACD+∠AED=165°,求∠ACD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com