
【题目】如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
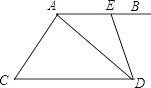
(1)求证:AD平分∠CDE;
(2)若AC⊥AD,∠ACD+∠AED=165°,求∠ACD的度数.
【答案】(1)见解析;(2)55°
【解析】
(1)根据平行线的性质得到∠BED=∠EDC,∠BAD=∠ADC,利用等量代换得到∠EDC=2∠ADC,由角平分线的定义即可得到结论;
(2)利用列方程的方式,设∠ADC=∠ADE=∠BAD=x,于是得到∠BED=∠EDC=2x,∠AED=180°-2x,根据平行线的性质得到∠BAC+∠ACD=180°,于是列方程90°-x+180°-2X=165°,即可得到结论.
(1)证明:∵AB∥CD,
∴∠BED=∠EDC,∠BAD=∠ADC,
∵∠BED=∠BAD+∠ADE,
∵∠BED=2∠BAD,
∴∠BAD=∠ADE,∠ADE=∠ACD,
∴AD平分∠CDE;
(2)解:依题意设∠ADC=∠ADE=∠BAD=x,
∴∠BED=∠EDC=2x,∠AED=180°﹣2x,
∵AB∥CD,
∴∠BAC+∠ACD=180°,即∠ACD=90°﹣x,
又∵∠ACD+∠AED=165°,
即90°﹣x+180°﹣2x=165°,
∴x=35°,
∴∠ACD=90°﹣x=90°﹣35°=55°.


科目:初中数学 来源: 题型:
【题目】某班去商场为书法比赛买奖品,书包每个定价40元,文具盒每个定价8元,商场实行两种优惠方案:①买一个书包送一个文具盒:②按总价的9折付款.若该班需购买书包10个,购买文具盒若干个(不少于10个).
(1)当买文具盒40个时,分别计算两种方案应付的费用;
(2)当购买文具盒多少个时,两种方案所付的费用相同;
(3)如何根据购买文具盒的个数,选择哪种优惠方案的费用比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
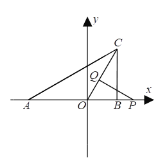
【题目】已知A(α,0)、B(b,0),点C在y轴上,且由|a+4|+(b-2)2=0.
(1)若S△ABC=6,求C点的坐标;
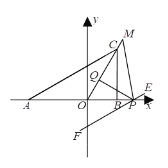
(2)将C向右平移,使OC平分∠ACB,点P是x轴上B点右边的一动点,PQ⊥OC于Q点.当∠ABC-∠BAC=60°时,求∠APQ的度数;
(3)在(2)的条件下,将线段AC平移,使其经过P点得线段EF,作∠APE的角平分线交OC的延长线于点M.当P点在x轴上运动时,求∠M-![]() ∠ABC的值.
∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF与六边形A′B′C′D′E′F′相似.
求:(1)相似比;
(2)∠A和∠B′的度数;
(3)边CD,EF,A′F′,E′D′的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,且M在AD上以1cm/s的速度由A向D运动,点N在BC上以2cm/s的速度由C向B运动.
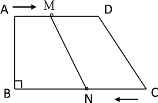
(1)几秒后MNCD为平行四边形?
(2)几秒后ABNM为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
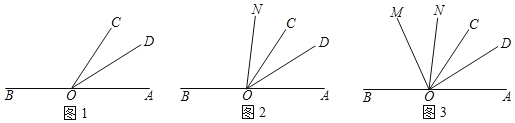
【题目】已知:点O为直线AB上一点,过点O作射线OC,使∠AOC=70°.
(1)如图1,若OD平分∠AOC,求∠DOB的度数;
(2)射线OM从OA出发,绕点O以每秒6°的速度逆时针旋转,同时,射线ON从OC出发绕点O以每秒4°的速度逆时针旋转,OM与ON同时出发(当ON首次与OB重合时,两条射线都停止运动),设运动的时间为t秒.
(i)如图2,在整个运动过程中,当∠BON=2∠COM时,求t的值;
(ⅱ)如图3,OP平分∠AOM,OQ平分∠BON,是否存在合适的t,使OC平分∠POQ,若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com