
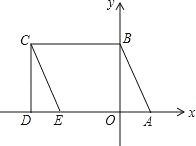
【题目】如图所示,A(2,0),点 B 在 y 轴上,将三角形 OAB 沿 x 轴负方向平移,平移后的图形为三角形 DEC,且点 C 的坐标为(-6,4) .
(1)直接写出点 E 的坐标 ;
(2)在四边形 ABCD 中,点 P 从点 B 出发,沿“BC→CD”移动.若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒,回答下列问题:
①求点 P 在运动过程中的坐标,(用含 t 的式子表示,写出过程);
②当 3 秒<t<5 秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z 之间的数量关系能否确定?若能,请用含 x,y 的式子表示 z,写出过程;若不能,说明理由.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班去商场为书法比赛买奖品,书包每个定价40元,文具盒每个定价8元,商场实行两种优惠方案:①买一个书包送一个文具盒:②按总价的9折付款.若该班需购买书包10个,购买文具盒若干个(不少于10个).
(1)当买文具盒40个时,分别计算两种方案应付的费用;
(2)当购买文具盒多少个时,两种方案所付的费用相同;
(3)如何根据购买文具盒的个数,选择哪种优惠方案的费用比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
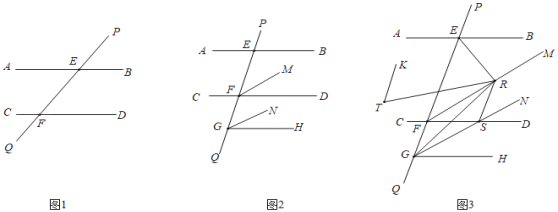
(1)如图1,求证:AB∥CD;
(2)如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;
(3)如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚准备用一段长 44 米的篱笆围成三角形,用于养鸡。已知一条边长 x 米,第二条边是第一条边的 3 倍多 6 米。
(1)若能围成一个等腰三角形,求三边长
(2)若第一边长最短,写出 x 的取值范围 。
查看答案和解析>>
科目:初中数学 来源: 题型:
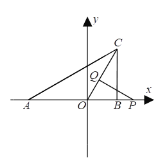
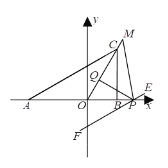
【题目】已知A(α,0)、B(b,0),点C在y轴上,且由|a+4|+(b-2)2=0.
(1)若S△ABC=6,求C点的坐标;
(2)将C向右平移,使OC平分∠ACB,点P是x轴上B点右边的一动点,PQ⊥OC于Q点.当∠ABC-∠BAC=60°时,求∠APQ的度数;
(3)在(2)的条件下,将线段AC平移,使其经过P点得线段EF,作∠APE的角平分线交OC的延长线于点M.当P点在x轴上运动时,求∠M-![]() ∠ABC的值.
∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,且M在AD上以1cm/s的速度由A向D运动,点N在BC上以2cm/s的速度由C向B运动.
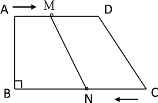
(1)几秒后MNCD为平行四边形?
(2)几秒后ABNM为矩形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com