
【题目】已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
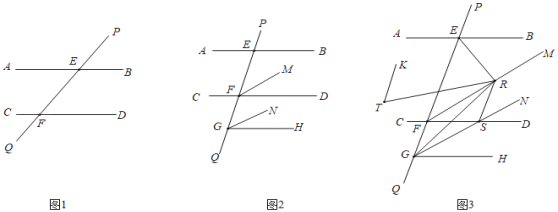
(1)如图1,求证:AB∥CD;
(2)如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;
(3)如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.
【答案】(1)见解析;(2)见解析;(3)∠NGH=32°.
【解析】
(1)根据邻补角的性质得∠PFD+∠QFD=180![]() ,再由同角的补角相等得∠PEB=∠PFD,最后由平行线的判定得结论;
,再由同角的补角相等得∠PEB=∠PFD,最后由平行线的判定得结论;
(2)先证GH∥CD,得∠EFD=∠FGH,再证∠EFM=∠FGN,便可得结论;
(3)先证明∠TRF=∠SRF,设∠SRG=x![]() ,由∠KTR+∠ERF=108
,由∠KTR+∠ERF=108![]() ,列出x的方程,求得x,便可得∠ERS,过R作RI∥AB,过点S作SL∥AB,则AB∥IR∥SL∥GH,通过平行线的性质,求得∠RSL,再由三角形外角定理得∠RSN,最后便可求得结果.
,列出x的方程,求得x,便可得∠ERS,过R作RI∥AB,过点S作SL∥AB,则AB∥IR∥SL∥GH,通过平行线的性质,求得∠RSL,再由三角形外角定理得∠RSN,最后便可求得结果.
(1)∵∠PEB+∠QFD=180![]() ,
,
又∵∠PFD+∠QFD=180![]() ,
,
∴∠PEB=∠PFD,
∴AB∥CD;
(2)∵GH∥AB,AB∥CD
∴GH∥CD,
∴∠EFD=∠FGH,
∵∠MFD=∠NGH,
∴∠EFM=∠FGN,
∴FM∥GN;
(3)∵FM∥GN,
∴∠FRG=∠SGR,
∵∠SGR=∠SRG,
∴∠FRG=∠SRG,
∵射线RT平分∠ERS,
∴∠ERT=∠TRS,
∵∠ERT=2∠TRF,
∴∠TRS=2∠TRF,
∴∠TRF=∠SRF,
设∠SRG=∠FRG=x![]() ,则∠TRF=2x
,则∠TRF=2x![]() ,∠ERT=∠SRT=4x
,∠ERT=∠SRT=4x![]() ,
,
∵TK∥RG,
∴∠KTR=∠TRG=2x![]() +x
+x![]() =3x
=3x![]() ,
,
∵∠KTR+∠ERF=108![]() ,
,
∴3x+4x+2x=108,
∴x=12![]() ,
,
∴∠ERS=8x=96![]() ,
,
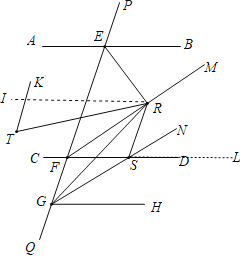
过R作RI∥AB,过点S作SL∥AB,则AB∥IR∥SL∥GH,
∴∠BER=∠ERI,∠IRS=∠RSL,∠NGH=∠NSL,
∵∠BER=40![]() ,
,
∴∠ERI=40![]() ,
,
∴∠RSL=∠IRS=∠ERS﹣∠ERI=96![]() ﹣40
﹣40![]() =56
=56![]() ,
,
∵∠RSN=∠SRG+∠SGR=24![]() ,
,
∴∠NGH=∠NSL=∠RSL﹣∠RSN=56![]() ﹣24
﹣24![]() =32
=32![]() .
.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】某学生本学期6次数学考试成绩如下表所示:
成绩类别 | 第一次月考 | 第二次月考 | 期中 | 第三次月考 | 第四次月考 | 期末 |
成绩/分 | 105 | 110 | 108 | 113 | 108 | 112 |
(1)6次考试成绩的中位数为 ,众数为 .
(2)求该生本学期四次月考的平均成绩.
(3)如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算,那么该生本学期的数学总评成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若AB是⊙O内接正五边形的一边,AC是⊙O内接正六边形的一边,则∠BAC等于( )
A. 120° B. 6° C. 114° D. 114°或6°
查看答案和解析>>
科目:初中数学 来源: 题型:
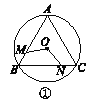
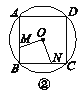
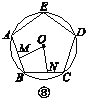
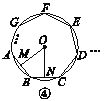
【题目】如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD交BD的延长线于点E,若BD=2,则CE=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
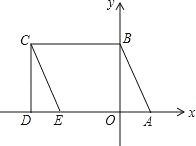
【题目】如图所示,A(2,0),点 B 在 y 轴上,将三角形 OAB 沿 x 轴负方向平移,平移后的图形为三角形 DEC,且点 C 的坐标为(-6,4) .
(1)直接写出点 E 的坐标 ;
(2)在四边形 ABCD 中,点 P 从点 B 出发,沿“BC→CD”移动.若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒,回答下列问题:
①求点 P 在运动过程中的坐标,(用含 t 的式子表示,写出过程);
②当 3 秒<t<5 秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z 之间的数量关系能否确定?若能,请用含 x,y 的式子表示 z,写出过程;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤HB平分∠AHD.其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
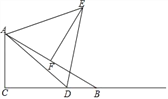
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com