
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD交BD的延长线于点E,若BD=2,则CE=_________.

【答案】1
【解析】
延长BA、CE相交于点F,利用“角边角”证明△BCE和△BFE全等,根据全等三角形对应边相等可得CE=EF,根据等角的余角相等求出∠ABD=∠ACF,然后利用“角边角”证明△ABD和△ACF全等,根据全等三角形对应边相等可得BD=CF,然后求解即可.
如图,延长BA、CE相交于点F,
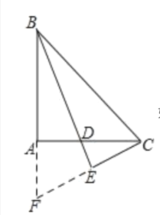
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△BCE和△BFE中,
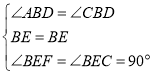 ,
,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90,
∴∠ABD=∠ACF,
在△ABD和△ACF中,
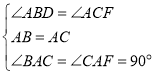 ,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CF=CE+EF=2CE,
∴BD=2CE=2,
∴CE=1.
故答案为:1.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,每辆车的月租金为4000元时,可全部租出.每辆车的月租金每增加100元,未租出的车将增加1辆.租出的车每辆每月的维护费为500元,未租出的车每辆每月只需维护费100元.
(1)当每辆车的月租金为4600元时,能租出多少辆?并计算此时租赁公司的月收益(租金收入扣除维护费)是多少万元?
(2)规定每辆车月租金不能超过7200元,当每辆车的月租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达40.4万元?
(3)当每辆车的月租金定为_________元时,租赁公司的月收益最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.
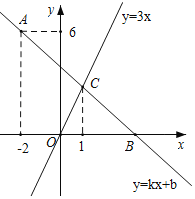
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
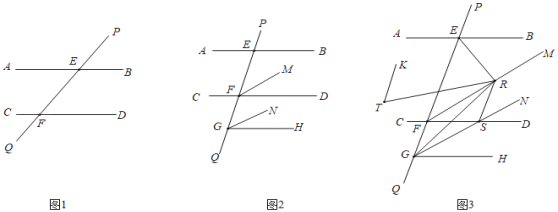
(1)如图1,求证:AB∥CD;
(2)如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;
(3)如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠1=∠2,EG 平分∠AEC.
(1)如图1,∠MAE=50°,∠FEG=15°,∠NCE=80°.试判断 EF 与 CD 的位置关系,并说明理由.
(2)如图2,∠MAE=135°,∠FEG=30°,当 AB∥CD 时,求∠NCE 的度数;
(3)如图2,试写出∠MAE、∠FEG、∠NCE 之间满足什么关系时,AB∥CD.
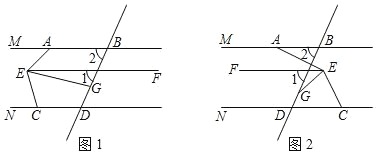
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学问题中,我们常用几何方法解决代数问题,借助数形结合的方法使复杂问题简单化.
材料一:我们知道|a|的几何意义是:数轴上表示数a的点到原点的距离;|a﹣b|的几何意义是:数轴上表示数a,b的两点之间的距离;|a+b|的几何意义是:数轴上表示数a,﹣b的两点之间的距离;根据绝对值的几何意义,我们可以求出以下方程的解.
(1)|x﹣3|=4
解:由绝对值的几何意义知:
在数轴上x表示的点到3的距离等于4
∴x1=3+4=7,x2=3﹣4=﹣1
(2)|x+2|=5
解:∵|x+2|=|x﹣(﹣2)|,∴其绝对值的几何意义为:在数轴上x表示的点到﹣2的距离等于5.∴x1=﹣2+5=3,x2=﹣2﹣5=﹣7
材料二:如何求|x﹣1|+|x+2|的最小值.
由|x﹣1|+|x+2|的几何意义是数轴上表示数x的点到表示数1和﹣2两点的距离的和,要使和最小,则表示数x的这点必在﹣2和1之间(包括这两个端点)取值.
∴|x﹣1|+|x+2|的最小值是3;由此可求解方程|x﹣1|+|x+2|=4,把数轴上表示x的点记为点P,由绝对值的几何意义知:当﹣2≤x≤1时,|x﹣1|+|x+2|恒有最小值3,所以要使|x﹣1|+|x+2|=4成立,则点P必在﹣2的左边或1的右边,且到表示数﹣2或1的点的距离均为0.5个单位.
故方程|x﹣1|+|x+2|=4的解为:x1=﹣2﹣0.5=﹣2.5,x2=1+0.5=1.5.
阅读以上材料,解决以下问题:
(1)填空:|x﹣3|+|x+2|的最小值为 ;
(2)已知有理数x满足:|x+3|+|x﹣10|=15,有理数y使得|y﹣3|+|y+2|+|y﹣5|的值最小,求x﹣y的值.
(3)试找到符合条件的x,使|x﹣1|+|x﹣2|+…+|x﹣n|的值最小,并求出此时的最小值及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点E,F分别在AB,CD上,AF⊥CE,垂足为点O,∠1=∠B,
∠A+∠2=90°.求证:AB∥CD.
证明:如图,
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
______________
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行)
请你仔细观察下列序号所代表的内容:
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
③∵AF⊥CE(已知)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
横线处应填写的过程,顺序正确的是( )
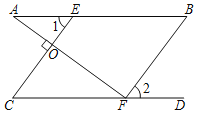
A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com