
【题目】已知:如图,点E,F分别在AB,CD上,AF⊥CE,垂足为点O,∠1=∠B,
∠A+∠2=90°.求证:AB∥CD.
证明:如图,
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
______________
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行)
请你仔细观察下列序号所代表的内容:
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
③∵AF⊥CE(已知)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
横线处应填写的过程,顺序正确的是( )
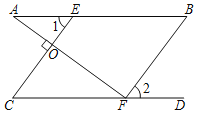
A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④
【答案】A
【解析】
先证CE∥BF得∠AOE=∠AFB,由AF⊥CE得∠AOE=∠AFB=90°,利用平角定义得出∠AFC+∠2=90°,结合∠A+∠2=90°可以得出∠AFC=∠A,从而得证.
证明:如图,
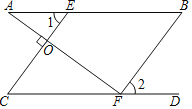
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
③∵AF⊥CE(已知)
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行),
故选:A.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD交BD的延长线于点E,若BD=2,则CE=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨辉是中国南宋末年的一位杰出的数学家,数学教育家.杨辉三角是杨辉的一大重要研究成果,其中蕴含了许多优美的规律.古今中外,许多的数学家都曾对其深入研究过,并将研究结果应用于实践.其中杨辉三角如下

(1)第5行的数和为________
(2)观察每行数的和,并归纳出第![]() 行数的和为________
行数的和为________
(3)第三斜行的数分别为1,3,6,10,…,请依此规律写出第5个数为 .请归纳得出第三斜行第![]() 个数的表达式________(用含有
个数的表达式________(用含有![]() 的表达式表示)
的表达式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
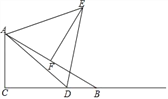
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是_____.
(k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是_____.
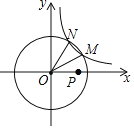
查看答案和解析>>
科目:初中数学 来源: 题型:
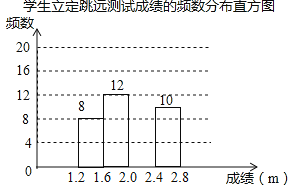
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1.例:[0.5]=﹣0.5.
(1)求[![]() ]、[﹣1]的值;
]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b],试求代数式(b﹣a)3﹣3a+3b的值;
(3)解方程:[x]+[x+2]=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,如果AD//BC,AE//CF,BE=DF,那么下列等式中错误的是( )
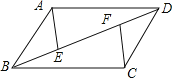
A. ∠DAE=∠BCFB. AB=CDC. ∠BAE=∠DCFD. ∠ABE=∠EBC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com