
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米处建有一个监测点P,道路AB段为检测区(如图).在△ABP中,已知∠PAB=32°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速?(精确到0.1秒.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆,![]() =
=![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
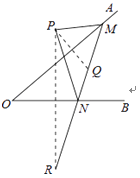
【题目】如下图,点![]() 是
是![]() 外的一点,点
外的一点,点![]() ,
,![]() 分别是
分别是![]() 两边上的点,点
两边上的点,点![]() 关于
关于![]() 的对称点
的对称点![]() 恰好落在线段
恰好落在线段![]() 上,点
上,点![]() 关于
关于![]() 的对称点
的对称点![]() 落在
落在![]() 的延长线上.若
的延长线上.若![]() ,
,![]() ,
,![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:

(1)楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市文化节期间,在景观湖中央搭建了一个舞台C,在岸边搭建了三个看台A,B,D,其中A,C,D三点在同一条直线上,看台A,B到舞台C的距离相等,测得∠A=30°,∠D=45°,AB=60 m,小明、小丽分别在B,D看台观看演出,请分别求出小明、小丽与舞台C的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生本学期6次数学考试成绩如下表所示:
成绩类别 | 第一次月考 | 第二次月考 | 期中 | 第三次月考 | 第四次月考 | 期末 |
成绩/分 | 105 | 110 | 108 | 113 | 108 | 112 |
(1)6次考试成绩的中位数为 ,众数为 .
(2)求该生本学期四次月考的平均成绩.
(3)如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算,那么该生本学期的数学总评成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若AB是⊙O内接正五边形的一边,AC是⊙O内接正六边形的一边,则∠BAC等于( )
A. 120° B. 6° C. 114° D. 114°或6°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤HB平分∠AHD.其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com