
【题目】已知a,b为有理数,且a,b不为0,则定义有理数对(a,b)的“真诚值”为d(a,b)= ,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
(1)求有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)求证:有理数对(a,b)与(b,a)的“真诚值”相等;
(3)若(a,2)的“真诚值”的绝对值为|d(a,2)|,若|d(a,2)|=6,求a的值.
【答案】(1)d(﹣3,2)的“真诚值”为﹣1,d(1,2)的“真诚值”为﹣9;(2)见解析;(3)见解析.
【解析】
(1)根据题目中的新定义,可以求得有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)根据题意分类讨论当a>b时和当a<b时,再结合新定义进行证明结论;
(3)由|d(a,2)|=6,得到d(a,2)=±6,分d(a,2)=6和d(a,2)=﹣6时进行讨论即可得到答案.
(1)d(﹣3,2)=(﹣3)2﹣10=9﹣10=﹣1,d(1,2)=12﹣10=1﹣10=﹣9;
(2)证明:由题知:
ⅰ当a>b时,因为d(a,b)=ba﹣10,d(b,a)=ba﹣10,
所以d(a,b)=d(b,a);
ⅱ当a<b时,因为d(a,b)=ab﹣10,(b,a)=ab﹣10,
所以d(a,b)=d(b,a);
综合所得:d(a,b)=d(b,a);
(3)因为|d(a,2)|=6,所以d(a,2)=±6,
ⅰ、若d(a,2)=6,
当a>2 时,2a﹣10=6,2a=16,得a=4成立;
当a<2 时,a2﹣10=6,a2=16,得a=±4,
因为a<2,所以a=﹣4;
ⅱ、若d(a,2)=﹣6时
当a>2 时,2a﹣10=﹣6,2a=4,得a=2不成立;
当a<2 时,a2﹣10=﹣6,a2=4,得a=±2,
因为a<2,所以a=﹣2;
由上可得,a=﹣2或±4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为( )
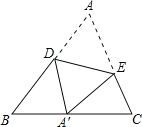
A. 35°B. 40°C. 45°D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A,B,C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是________.
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
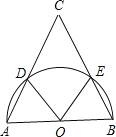
【题目】如图,已知点O为等腰三角形ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.
求证:(1)∠AOE=∠BOD;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
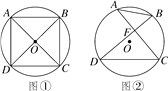
【题目】已知A,B,C,D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图②,若AC⊥BD,垂足为F,AB=2,DC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为![]() 分(
分(![]() ).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
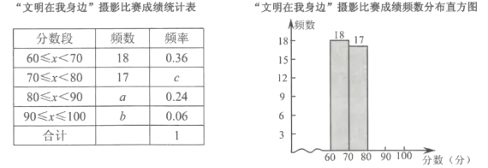
根据以上信息解答下列问题:
(1)统计表中![]() 的值为 ;样本成绩的中位数落在分数段 中;
的值为 ;样本成绩的中位数落在分数段 中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
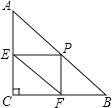
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,P为AB边上不与A,B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .(1)若点
.(1)若点![]() 恰好落在
恰好落在![]() 边上,则
边上,则![]() ______,(2)延长
______,(2)延长![]() 交直线
交直线![]() 于点
于点![]() ,已知
,已知![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店,准备用不超过2800元购买足球和篮球共计60个,已知一个篮球的进价为50元,售价为65元;一个足球的进价为40元,售价为50元.
(1)若购进x个篮球,购买这批球共花费y元,求y与x之间的函数关系式;
(2)设售出这批球共盈利w元,求w与x之间的函数关系式;
(3)体育用品商店购进篮球和足球各多少个时,才能获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com