
【题目】在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .(1)若点
.(1)若点![]() 恰好落在
恰好落在![]() 边上,则
边上,则![]() ______,(2)延长
______,(2)延长![]() 交直线
交直线![]() 于点
于点![]() ,已知
,已知![]() ,则
,则![]() ______.
______.
【答案】6 ![]() 或
或![]()
【解析】
(1)由矩形的性质得出![]() ,
,![]() ,由折叠的性质得出
,由折叠的性质得出![]() ,由平行线的性质得出
,由平行线的性质得出![]() ,推出
,推出![]() ,得出
,得出![]() ,即可得出结果;
,即可得出结果;
(2)①当点![]() 在矩形
在矩形![]() 内时,连接
内时,连接![]() ,由折叠的性质得出
,由折叠的性质得出![]() ,
,![]() ,
,![]() ,由矩形的性质和
,由矩形的性质和![]() 是
是![]() 的中点,得出
的中点,得出![]() ,
,![]() ,
,![]() ,由
,由![]() 证得
证得![]() ,得出
,得出![]() ,由
,由![]() ,得出
,得出![]() ,
,![]() ,
,![]() ,由勾股定理即可求出
,由勾股定理即可求出![]() ;
;
②当点![]() 在矩形
在矩形![]() 外时,连接
外时,连接![]() ,由折叠的性质得出
,由折叠的性质得出![]() ,
,![]() ,
,![]() ,由矩形的性质和
,由矩形的性质和![]() 是
是![]() 的中点,得出
的中点,得出![]() ,
,![]() ,
,![]() ,由
,由![]() 证得
证得![]() ,得出
,得出![]() ,由
,由![]() ,得出
,得出![]() ,由勾股定理得出:
,由勾股定理得出:![]() ,即
,即![]() ,即可求出
,即可求出![]() .
.
解:(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
由折叠的性质可知,![]() ,如图1所示:
,如图1所示:
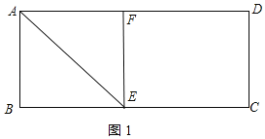
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
(2)①当点![]() 在矩形
在矩形![]() 内时,连接
内时,连接![]() ,如图2所示:
,如图2所示:
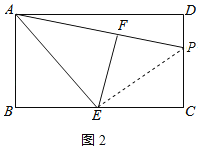
由折叠的性质可知,![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
②当点![]() 在矩形
在矩形![]() 外时,连接
外时,连接![]() ,如图3所示:
,如图3所示:
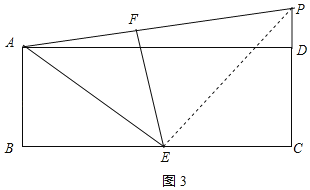
由折叠的性质可知,![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即:![]() ,
,
![]() ,
,
解得:![]() ,
,![]() (不合题意舍去),
(不合题意舍去),
综上所述,![]() 或
或![]() ,
,
故答案为:(1)6;(2)![]() 或
或![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且满足
,且满足![]() ,多项式
,多项式![]() 是五次四项式.
是五次四项式.
(1)![]() 的值为 ,
的值为 ,![]() 的值为 ,
的值为 ,![]() 的值为 .
的值为 .
(2)已知点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 以每秒3个单位的速度向右运动,同时点
以每秒3个单位的速度向右运动,同时点![]() 从点
从点![]() 出发,以每秒7个单位的速度向左运动:
出发,以每秒7个单位的速度向左运动:
①若点![]() 从点
从点![]() 出发,点
出发,点![]() 和点
和点![]() 经过
经过![]() 秒后,在数轴上的点
秒后,在数轴上的点![]() 处相遇,求
处相遇,求![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
②若点![]() 先从点
先从点![]() 出发,运动到点
出发,运动到点![]() 处,点
处,点![]() 再出发,则点
再出发,则点![]() 运动几秒后两点之间的距离为5个单位长度?
运动几秒后两点之间的距离为5个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b为有理数,且a,b不为0,则定义有理数对(a,b)的“真诚值”为d(a,b)= ,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
(1)求有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)求证:有理数对(a,b)与(b,a)的“真诚值”相等;
(3)若(a,2)的“真诚值”的绝对值为|d(a,2)|,若|d(a,2)|=6,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是______.(把所有正确结论的序号都填在横线上)①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
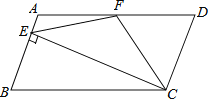
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,每辆车的月租金为4000元时,可全部租出.每辆车的月租金每增加100元,未租出的车将增加1辆.租出的车每辆每月的维护费为500元,未租出的车每辆每月只需维护费100元.
(1)当每辆车的月租金为4600元时,能租出多少辆?并计算此时租赁公司的月收益(租金收入扣除维护费)是多少万元?
(2)规定每辆车月租金不能超过7200元,当每辆车的月租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达40.4万元?
(3)当每辆车的月租金定为_________元时,租赁公司的月收益最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
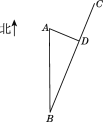
【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?
查看答案和解析>>
科目:初中数学 来源: 题型:
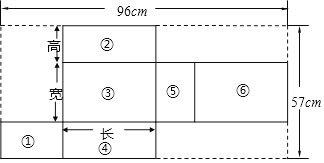
【题目】如图是某涌泉蜜桔长方体包装盒的展开图.具体数据如图所示,且长方体盒子的长是宽的2倍.
(1)展开图的6个面分别标有如图所示的序号,若将展开图重新围成一个包装盒,则相对的面分别是 与 , 与 , 与 ;
(2)若设长方体的宽为xcm,则长方体的长为 cm,高为 cm;(用含x的式子表示)
(3)求这种长方体包装盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠1=∠2,EG 平分∠AEC.
(1)如图1,∠MAE=50°,∠FEG=15°,∠NCE=80°.试判断 EF 与 CD 的位置关系,并说明理由.
(2)如图2,∠MAE=135°,∠FEG=30°,当 AB∥CD 时,求∠NCE 的度数;
(3)如图2,试写出∠MAE、∠FEG、∠NCE 之间满足什么关系时,AB∥CD.
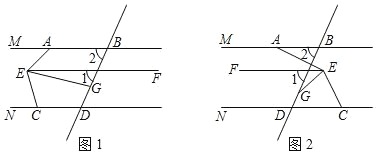
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com