
【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.
如:①用配方法分解因式:a2+6a+8,
解:原式=a2+6a+8+1﹣1=a2+6a+9﹣1=(a+2)(a+4)
②M=a2﹣2ab+2b2﹣2b+2,利用配方法求M的最小值,
解:a2﹣2ab+2b2﹣2b+2=a2﹣2ab+b2+b2﹣2b+1+1=(a﹣b)2+(b﹣1)2+1
∵(a﹣b)2≥0,(b﹣1)2≥0
∴当a=b=1时,M有最小值1.
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:x2﹣![]() x+ .
x+ .
(2)用配方法因式分解:x2﹣4xy+3y2.
(3)若M=![]() x2+2x﹣1,求M的最小值.
x2+2x﹣1,求M的最小值.
(4)已知x2+2y2+z2﹣2xy﹣2y﹣4z+5=0,则x+y+z的值为 .
【答案】(1)![]() ;(2)(x﹣y)(x﹣3y);(3)当x=﹣4时,M有最小值为﹣5;(4)4.
;(2)(x﹣y)(x﹣3y);(3)当x=﹣4时,M有最小值为﹣5;(4)4.
【解析】
(1)加一次项系数一半的平方,可配成完全平方式;
(2)将3y2化成4y2y2,前三项配成完全平方式,再利用平方差公式进行因式分解;
(3)提取系数![]() 后,再加一次项系数一半的平方16,并减去16,配成完全平方式,可知M的最小值;
后,再加一次项系数一半的平方16,并减去16,配成完全平方式,可知M的最小值;
(4)拆项后配成三个完全平方式,利用非负数的性质求出x、y、z的值,然后相加即可.
解:(1)x2﹣![]() x+
x+![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)x2﹣4xy+3y2
=x2﹣4xy+4y2﹣y2
=(x﹣2y)2﹣y2
=(x﹣2y+y)(x﹣2y﹣y)
=(x﹣y)(x﹣3y);
(3)M=![]() x2+2x﹣1=
x2+2x﹣1=![]() (x2+8x+16﹣16)﹣1=
(x2+8x+16﹣16)﹣1=![]() (x+4)2﹣5,
(x+4)2﹣5,
∵![]() (x+4)2≥0,
(x+4)2≥0,
∴当x=﹣4时,M有最小值为﹣5;
(4)∵x2+2y2+z2﹣2xy﹣2y﹣4z+5=0,
∴x2﹣2xy+y2+y2﹣2y+1+z2﹣4z+4=0,
∴(x﹣y)2+(y﹣1)2+(z﹣2)2=0,
∴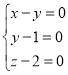 ,
,
∴x=1,y=1,z=2,
∴x+y+z=1+1+2=4,
故答案为:4.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
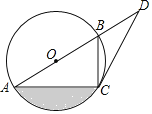
【题目】如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
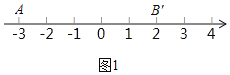
【题目】(1)对数轴上的点P进行如下操作:先把点P表示的数乘以![]() ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴t,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是 ,若点B′表示的数是2,则点B表示的数是 ;已知线段AB上的点E经过上述操作后得到的对应点E'点E重合,则点E表示的数是 .
,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴t,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是 ,若点B′表示的数是2,则点B表示的数是 ;已知线段AB上的点E经过上述操作后得到的对应点E'点E重合,则点E表示的数是 .
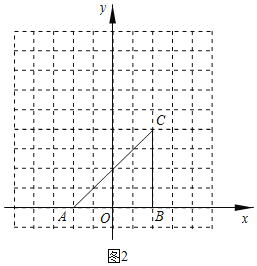
(2)在平面直角坐标系xOy中,已知△ABC的顶点A(﹣2,0),B(2,0),C(2,4),对△ABC及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同个实数a,将得到的点先向右平移m单位,冉向上平移n个单位(m>0,n>0),得到△ABC及其内部的点,其中点A,B的对应点分别为A′(1,2),B′(3,2).△ABC内部是否存在点F,使得点F经过上述操作后得到的对应点F′与点F重合,若存在,求出点F的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粮库3天内发生粮食进出库的吨数如下(+表示进库-表示出库)+26,-32,-15,+34,-38,-20
(1)经过这3天,库里的粮食是增多还是减少了?
(2)经过这3天,仓库管理员结算发现库里还存480吨粮,那么3天前库里存粮多少吨?
(3)如果进出的装御费都是每吨5元,那么这3天要付多少装卸费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例函数y=![]() (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
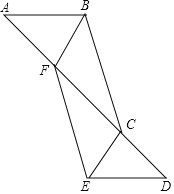
【题目】如图,在△ABC和△DEF中,AB∥DE,点A,F,C,D在同一直线上,AF=CD,∠AFE=∠BCD.
试说明:
(1)△ABC≌△DEF;
(2)BF∥EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若反比例函数y=![]() (k≠0)的图像经过点P(-4,5),则该函数的图像不经过的点是( )
(k≠0)的图像经过点P(-4,5),则该函数的图像不经过的点是( )
A. (-5,4) B. (-2,10) C. (10,-2) D. (-10,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学家的饮水机中原有水的温度为20 ℃,其工作过程如图所示.在一个由20 ℃加热到100 ℃再降温到20 ℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.
(1)写出水温下降过程中y与x之间的函数表达式,并求出x为何值时,y=100;
(2)求加热过程中y与x之间的函数表达式;
(3)求当x为何值时,y=80.
问题解决
若嘉淇同学上午八点将饮水机通电开机后立刻外出散步,预计九点前回到家中,若嘉淇想喝到不低于50 ℃的水,则直接写出她外出的时间m(分)的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com