
| 时间项目 | 用水量(m3) | 费用(元) |
| 11月 | 15 | 35 |
| 12月 | 18 | 44 |
分析 设正常收费标准为x元/m3,超过部分y元/m3.等量关系:①用水量是15m3时,费用35元;②用水量是18m3时,费用是44元.
解答 解:设正常收费标准为x元/m3,超过部分y元/m3.
由题意,得$\left\{\begin{array}{l}{10x+(15-10)y=35}\\{10x+(18-10)y=44}\end{array}\right.$,
解得,
$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
答:正常收费标准为2元/m3,超过部分3元/m3.
点评 此题考查了二元一次方程组在实际问题中的应用,能够从表格中获得正确信息,注意收费标准的分类.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
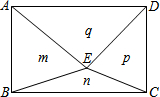 如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m+n)2(m-n) | B. | (m+n)3(m-n) | C. | (m+n)(m-n) | D. | (m2-n2)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com