
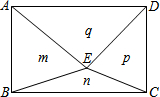
 如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
分析 过E作MN⊥AB,交AB于M,CD于N,作GH⊥AD,交AD于G,BC于H,由矩形的性质容易证出①不正确,②正确;若m=n,则p=q,作AP⊥BE于P,作CQ⊥DE于Q,延长BE交CD于F,先证AP=CQ,再证明△ABP≌△CFQ,得出AB=CF,F与D重合,得出③不正确,④正确,即可得出结论.
解答 解:过E作MN⊥AB,交AB于M,CD于N,作GH⊥AD,交AD于G,BC于H,如图1所示: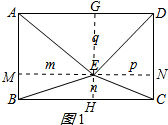
则m=$\frac{1}{2}$AB•EM,n=$\frac{1}{2}$BC•EH,p=$\frac{1}{2}$CD•EN,q=$\frac{1}{2}$AD•EG,
∵四边形ABCD是矩形,
∴AB=CD=GH,BC=AD=MN,
∴m+p=$\frac{1}{2}$AB•MN=$\frac{1}{2}$AB•BC,n+q=$\frac{1}{2}$(BC•GH=$\frac{1}{2}$BC•AB,
∴m+p=n+q;
∴①不正确,②正确;
若m=n,则p=q,作AP⊥BE于P,作CQ⊥BE于Q,延长BE交CD于F,如图2所示: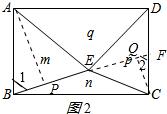
则∠APB=∠CQF=90°,
∵m=$\frac{1}{2}$BE•AP,n=$\frac{1}{2}$BE•CQ,
∵m=n,
∴AP=CQ,
∵AB∥CD,
∴∠1=∠2,
在△ABP和△CFQ中,
$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{∠APB=∠CQF}&{\;}\\{AP=CQ}&{\;}\end{array}\right.$,
∴△ABP≌△CFQ(AAS),
∴AB=CF,
∴F与D重合,
∴E一定在BD上;
∴③不正确,④正确.
故选:B.
点评 本题考查了矩形的性质、三角形面积的计算、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 时间项目 | 用水量(m3) | 费用(元) |
| 11月 | 15 | 35 |
| 12月 | 18 | 44 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
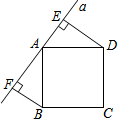 如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E.若DE=7,BF=5,则EF的长为12.
如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E.若DE=7,BF=5,则EF的长为12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
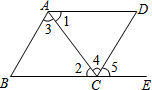 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )| A. | ①②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com