
 (1)先化简,再求值:$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$,其中x=2015.
(1)先化简,再求值:$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$,其中x=2015.分析 (1)根据分式加减的法则化简即可.
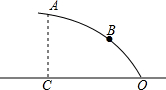
(2)①以点O为原点、射线OC为y轴的正半轴建立直角坐标系,可设抛物线的函数解析式为y=ax2,又由点A在抛物线上,即可求得此抛物线的函数解析式;
②延长AC,交建筑物造型所在抛物线于点D,连接BD交OC于点P,则点P即为所求;
解答 解:(1)$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$=$\frac{{x}^{2}-2x}{x-1}$+$\frac{1}{x-1}$=$\frac{{x}^{2}-2x+1}{x-1}$=$\frac{(x-1)^{2}}{x-1}$=x-1,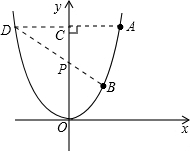
把x=2015代入,原式=2015-1=2014.
(2)以点O为原点、射线OC为y轴的正半轴建立直角坐标系,
设抛物线的函数解析式为y=ax2,
由题意知点A的坐标为(4,8).
∵点A在抛物线上,
∴8=a×42,
解得a=$\frac{1}{2}$,
∴所求抛物线的函数解析式为:y=$\frac{1}{2}$x2;
(2)作法:延长AC,交建筑物造型所在抛物线于点D,
则点A、D关于OC对称.
连接BD交OC于点P,则点P即为所求.
点评 (1)考查了分式的化简求值,熟练掌握分式加减的法则是解决问题的关键.
(2)此题考查了二次函数的实际应用问题.解此题的关键是根据题意构建二次函数模型,然后根据二次函数解题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
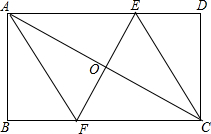 如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.
如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
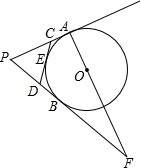 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
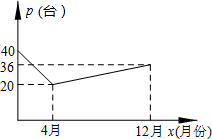 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
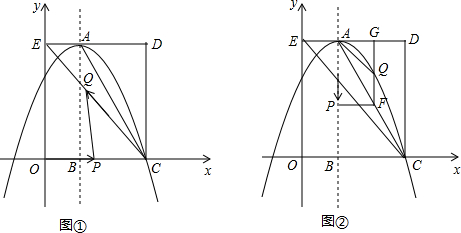
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
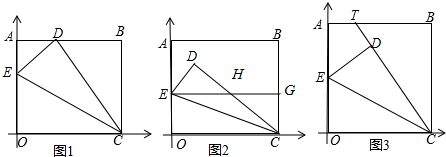
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
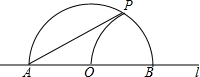 如图,直线l上一点O,以O为圆心,任意长为半径画半圆,交l于A、B两点,再以B为圆心,OB的长为半径画弧交半圆于P,连AP,则sin∠PAB的值等于$\frac{1}{2}$.
如图,直线l上一点O,以O为圆心,任意长为半径画半圆,交l于A、B两点,再以B为圆心,OB的长为半径画弧交半圆于P,连AP,则sin∠PAB的值等于$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com