
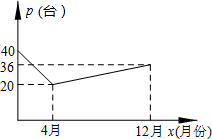
 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.分析 (1)要根据自变量的不同取值范围,运用待定系数法分段计算出p与x的函数关系式;
(2)可根据实际销售利润=单件的利润×销售的数量,然后根据题目中给出的售价与月次的函数式以及(1)中销售量与月次的关系式,得出实际销售利润与月次的函数关系式,根据自变量的不同的取值范围分别进行讨论,然后找出最高售价.
解答 解:(1)p=$\left\{\begin{array}{l}{-5x+40(1≤x<4且x为整数)}\\{2x+12(4≤x≤12且x为整数)}\end{array}\right.$,
(2)①当1≤x<4时,
w=(-0.05x+0.4-0.1)×(-5x+40)
=$\frac{1}{4}$(x-6)(x-8)=$\frac{1}{4}$x2-$\frac{7}{2}$x+12
∵a=$\frac{1}{4}$>0,-$\frac{b}{2a}$=7>4,
∴当1≤x<4时,w随x的增大而减小,
∴当x=1时取得w的最大值为:
$\frac{1}{4}$×12-$\frac{14}{4}$×1+12=8.75 (万元).
②当4≤x≤12时,
w=(0.2-0.1)×(2x+12)=$\frac{1}{5}$x+$\frac{6}{5}$
∵k=$\frac{1}{5}$>0,∴当4≤x≤12时,w随x的增大而增大,
∴当x=12时取得w的最大值为3.6:
$\frac{1}{5}$×12+$\frac{6}{5}$=3.6 (万元).
综上得:全年中1月份的实际销售利润w最高为8.75万元.
点评 本题是利用一次函数的有关知识解答实际应用题,由此看来一次函数是常用的解答实际问题的数学模型,是中考的常见题型.借助函数图象表达题目中的信息,读懂图象是关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$或-2 | B. | $\frac{1}{2}$或2 | C. | -2或$\frac{1}{2}$ | D. | -$\frac{1}{2}$或2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
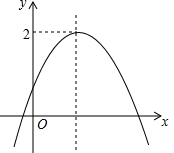 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论:| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
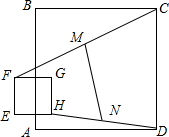 如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.
如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 360 | B. | 339 | C. | 440 | D. | 483 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)先化简,再求值:$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$,其中x=2015.
(1)先化简,再求值:$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$,其中x=2015.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.34×104 | B. | 13.4×104 | C. | 1.34×105 | D. | 0.134×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
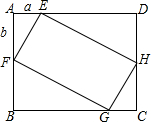 如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )| A. | $\left\{\begin{array}{l}{a+b=4}\\{a+2b=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2a+b=4}\\{a+2b=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=2b}\\{2a+b=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2a+b=5}\\{a+2b=4}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com